Cho hình chóp SABCD có đáy là hình thang vuông tại A;B với BC là đáy nhỏ. Biết rằng tam giác SAB đều có cạnh là 2a và nằm trong mặt phẳng vuông góc với đáy,
S
C
=
a
5
và khoảng cách từ D tới mặt phẳng (SHC) là
2
a
2
(H là trung điểm của AB). Thể tích khối chóp S.ABCDlà: A.
a
3
3
3
B.
a
3
3
C.
4
a
...
Đọc tiếp
Cho hình chóp SABCD có đáy là hình thang vuông tại A;B với BC là đáy nhỏ. Biết rằng tam giác SAB đều có cạnh là 2a và nằm trong mặt phẳng vuông góc với đáy, S C = a 5 và khoảng cách từ D tới mặt phẳng (SHC) là 2 a 2 (H là trung điểm của AB). Thể tích khối chóp S.ABCDlà:
A. a 3 3 3
B. a 3 3
C. 4 a 3 3 3
D. 4 a 3 3
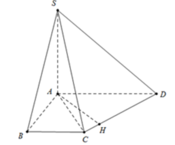
Đáp án là C
ta có S A B ⊥ A B C D S A B ∩ A B C D = A B S H ⊥ A B ⇒ S H ⊥ A B C D
mà D I ⊥ C H D I ⊥ S H ⇒ D I ⊥ S H C ⇒ d D , S H C = D I = 2 a 2
ta có
Δ B H C = Δ A H E ⇒ S Δ B H C = S Δ A H E ; H E = H C
mà
S A B C D = S A H C D + S Δ B H C = S A H C D + S Δ A H E = S Δ D C E
Tam giác SAB đều nên . S H = a 3
Tam giác SHC có
H C = S C 2 − S H 2 = a 2 ⇒ E C = 2 H C = 2 a 2 .
Khi đó S A B C D = S Δ D C E = 1 2 D I . E C = 4 a 2 .
Vậy V A B C D = 1 3 S H . S A B C D = 1 3 a 3 .4 a 2 = 4 a 3 3 3 .