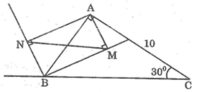
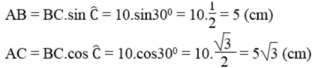Cho tam giác ABC vuông góc ở A. Biết AB =10cm; AC =15cm . Trên BC lấy trung điểm M, trên Ac lấy điểm D sao cho DC =1/3 AC. Nối B với D A với M cắt nhau tại I . Tính diện tích tứ giác IMCD ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=10^2-6^2=64\)
hay AC=8(cm)
Vậy: AC=8cm
b) Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)(BE là tia phân giác của \(\widehat{ABH}\))
Do đó: ΔABE=ΔHBE(cạnh huyền-góc nhọn)

Do tam giác ABC vuông tại A nên góc A là góc lớn nhất
Có AB < AC ⇒ C < B . Từ đó suy ra ∠C < ∠B < ∠A hay ∠A > ∠B > ∠C . Chọn B

a, Ta có: AB là cạnh đối diện của góc C.
AC là cạnh đối diện của góc B.
Mà AB>AC, suy ra:
góc B< góc C.
Áp dụng Đ. L. py-ta-go vào tg ABC vuông tại A, có:
BC2=AC2+AB2
=>102=62+AB2
=>AB2=102-62
=100-36
=64.

BC=10cm nên AB+AC=14cm
mà AB=3/4AC
nên 7/4AC=14cm
=>AC=8(cm)
=>AB=6(cm)
\(S_{ABC}=\dfrac{8\cdot6}{2}=24\left(cm^2\right)\)

Lời giải:
Tổng độ dài 2 cạnh góc vuông: $24-10=14$ (cm)
Tổng số phần bằng nhau (của 2 cạnh góc vuông): $3+4=7$ (phần)
Cạnh góc vuông thứ nhất: $14:7\times 3=6$ (cm)
Cạnh góc vuông thức hai: $14:7\times 4=8$ (cm)
Diện tích hình tam giác: $6\times 8:2=24$ (cm2)

Lời giải:
Ta có: $\tan B=\frac{AC}{AB}=\frac{10}{6}=\frac{5}{3}$
$\Rightarrow \widehat{B}=59,04^0$