Cho tam giác ABC (Góc BAC <90 độ)Đường cao AH .Gọi E,F lần lượt là điểm đối xứng của H qua AB ;AC,đường thẳng EF cắt AB:AC lần lượt tai M và N.Chứng minh rằng: a, AE=AF b,HA là phân giác của góc MHN c,CM song song với EH d,CM song song với EH ; BN song song với FH
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn tham khảo ở đường link sau:
https://olm.vn/hoi-dap/tim-kiem?q=cho+tam+gi%C3%A1c+ABC+(+g%C3%B3c+BAC=+90+%C4%91%E1%BB%99+)+,+AH+vu%C3%B4ng+g%C3%B3c+v%E1%BB%9Bi+BC.g%E1%BB%8Di+E+v%C3%A0+F+l%E1%BA%A7n+l%C6%B0%E1%BB%A3t+l%C3%A0+c%C3%A1c+%C4%91i%E1%BB%83m+%C4%91%E1%BB%91i+x%E1%BB%A9ng+c%E1%BB%A7a+H+qua+AB;AC+.+%C4%91%C6%B0%E1%BB%9Dng+th%E1%BA%B3ng+EF+c%E1%BA%AFt+B;C+l%E1%BA%A7n+l%C6%B0%E1%BB%A3t+t%E1%BA%A1i+M+v%C3%A0+N+.CMR+:+a)+AE=AFB)+HA+l%C3%A0+ph%C3%A2n+gi%C3%A1c+c%E1%BB%A7a+g%C3%B3c+MHNc)+Chung+minh+:+CM+song+song+v%E1%BB%9Bi+EH&id=455200

https://olm.vn/hoi-dap/tim-kiem?q=cho+tam+gi%C3%A1c+ABC+(+g%C3%B3c+BAC=+90+%C4%91%E1%BB%99+)+,+AH+vu%C3%B4ng+g%C3%B3c+v%E1%BB%9Bi+BC.g%E1%BB%8Di+E+v%C3%A0+F+l%E1%BA%A7n+l%C6%B0%E1%BB%A3t+l%C3%A0+c%C3%A1c+%C4%91i%E1%BB%83m+%C4%91%E1%BB%91i+x%E1%BB%A9ng+c%E1%BB%A7a+H+qua+AB;AC+.+%C4%91%C6%B0%E1%BB%9Dng+th%E1%BA%B3ng+EF+c%E1%BA%AFt+B;C+l%E1%BA%A7n+l%C6%B0%E1%BB%A3t+t%E1%BA%A1i+M+v%C3%A0+N+.CMR+:+a)+AE=AFB)+HA+l%C3%A0+ph%C3%A2n+gi%C3%A1c+c%E1%BB%A7a+g%C3%B3c+MHNc)+Chung+minh+:+CM+song+song+v%E1%BB%9Bi+EH&id=455200
Bạn tham khảo đường link trên nha, kéo xuống bên dưới đó, mình giải đc rồi nhưng dài quá ko gõ đc :))
À ở câu a) thì cách làm ở link trên đúng và ngắn hơn cách mình làm, còn đây là câu a) của mình nè:
a) Gọi EH cắt AB tại X, FH cắt AC tại Y
Vì E đối xứng với H qua AB nên EH vuông góc AB; EX=XH
Xét tam giác AEX và AHX có:
AX: cạnh chung
EX=XH (cmt)
Góc EXA = góc AXH (=90°)
Suy ra: tam giác AEX = tam giác AHX (c-g-c)
Do đó: AE=AH (2 cạnh tương ứng) (1)
Vì F đối xứng với H qua AC nên FH vuông góc AC; HY=YF
Xét tam giác AHY và AFY có:
HY=YF (cmt)
AY: cạnh chung
Góc AYH = góc AYF (=90°)
Suy ra: tam giác AHY = tam giác AFY (c-g-c)
Do đó: AH=AF (2 cạnh tương ứng) (2)
Từ (1) và (2) suy ra: AE=AF(=AH) (đpcm)
*Bạn tự viết kí hiệu góc, tam giác,...v.v... dùm mình nha, mình ko biết viết*

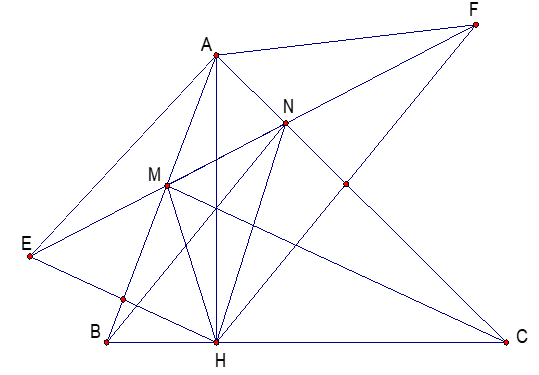
a. Vì AB là trung trực của EH nên ta có: AE = AH (1)
Vì AC là trung trực của HF nên ta có: AH = AF (2
Từ (1) và (2) suy ra: AE = AF
b.

c.


a. Vì AB là trung trực của EH nên ta có: AE = AH (1)
Vì AC là trung trực của HF nên ta có: AH = AF (2)
Từ (1) và (2) suy ra: AE = AF
b.
. 
c.
