Cho ∆ABC vuông tại A có AD là phân giác B̂AC; AB = √3 và AD = 3.
Tính...
Đọc tiếp
Cho ∆ABC vuông tại A có AD là phân giác B̂AC; AB = √3 và AD = 3.
Tính ÂDB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
B
1
Những câu hỏi liên quan
3 tháng 12 2023
a: Xét ΔABH có BI là phân giác
nên \(\dfrac{AI}{AB}=\dfrac{IH}{BH}\)
Xét ΔABC có BD là phân giác
nên \(\dfrac{AD}{AB}=\dfrac{CD}{CB}\)
Đề bài này chưa đủ dữ kiện để tính cụ thể AI/AB; AD/AB nha bạn
b: ΔBAD vuông tại A
=>\(\widehat{ABD}+\widehat{ADB}=90^0\)
=>\(\widehat{ADI}+\dfrac{1}{2}\cdot\widehat{ABC}=90^0\left(1\right)\)
ΔBIH vuông tại H
=>\(\widehat{HBI}+\widehat{BIH}=90^0\)
=>\(\widehat{BIH}+\dfrac{1}{2}\cdot\widehat{ABC}=90^0\)(2)
Từ (1) và (2) suy ra \(\widehat{ADI}=\widehat{BIH}\)
mà \(\widehat{AID}=\widehat{BIH}\)(hai góc đối đỉnh)
nên \(\widehat{ADI}=\widehat{AID}\)
=>ΔAID cân tại A
=>AD=AI(3)
Xét ΔABH có BI là phân giác
nên \(\dfrac{IH}{BH}=\dfrac{AI}{AB}\left(4\right)\)
Xét ΔABC có BD là phân giác
nên \(\dfrac{DC}{BC}=\dfrac{DA}{AB}\left(5\right)\)
Từ (3),(4),(5) suy ra \(\dfrac{IH}{BH}=\dfrac{DC}{BC}\)
31 tháng 8 2023
ΔABC vuông tại A
=>BC^2=AB^2+AC^2
=>\(BC=\sqrt{9^2+12^2}=15\left(cm\right)\)
Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/3=CD/4
mà BD+CD+15
nên \(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{15}{7}\)
=>BD=45/7(cm)
Xét ΔABC có AD là phân giác
nên \(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos\left(\dfrac{BAC}{2}\right)\)
\(=\dfrac{2\cdot9\cdot12}{9+12}\cdot\dfrac{\sqrt{2}}{2}=\dfrac{36\sqrt{2}}{7}\left(cm\right)\)
ΔABC vuông tại A có AK là đường cao
nên AK*BC=AB*AC
=>AK*15=12*9=108
=>AK=7,2cm
ΔAKD vuông tại K
=>AK^2+KD^2=AD^2
=>KD^2=AD^2-AK^2=1296/1225
=>KD=36/35(cm)
17 tháng 5 2021
△ABC có AD là đường phân giác
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{DB}{DC}=\dfrac{15}{20}=\dfrac{3}{4}\\ \Rightarrow\dfrac{AB^2}{AC^2}=\dfrac{9}{16}\\ \Rightarrow\dfrac{AB^2}{9}=\dfrac{AC^2}{16}=\dfrac{BC^2}{25}=\dfrac{\left(15+20\right)^2}{25}=49\\ \Rightarrow AB=\sqrt{49.9}=21\left(cm\right)\\ AC=\sqrt{49.16}=28\left(cm\right)\)
△ABC vuông tại A có \(AH\perp BC\)
\(\Rightarrow AH.BC=AB.AC\\ \Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{21.28}{35}=16,8\left(cm\right)\)
△ABC vuông tại A có \(AH\perp BC\)
\(\Rightarrow AB^2=AH.HB\\ \Rightarrow HB=\dfrac{AB^2}{AH}=\dfrac{21^2}{16,8}=26,25\left(cm\right)\\ HC=BC-HB=15+20-26,25=8,75\left(cm\right)\)
NT
0
23 tháng 6 2021
Kẻ \(AH\perp BC\) tại H
Áp dụng hệ thức lượng trong tam giác vuông BAC có:
\(\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{AH^2}\)
Do AD và AE lần lượt là hai tia phân giác trong và ngoài tại đỉnh A
\(\Rightarrow AD\perp AE\)
Áp dụng hệ thức lượng vào tam giác vuông AED có:
\(\dfrac{1}{AE^2}+\dfrac{1}{AD^2}=\dfrac{1}{AH^2}\) (AH là đường cao của tam giác AED do \(AH\perp BC\) hay \(AH\perp ED\))
\(\Rightarrow\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{AE^2}+\dfrac{1}{DA^2}\)
Vậy...
CM
11 tháng 3 2017
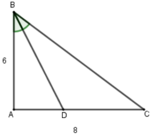
Tam giác ABC vuông tại A, áp dụng định lý Pytago có: B C 2 = A B 2 + A C 2
BD là tia phân giác góc B nên D A D C = B A B C = 6 10 = 3 5 ⇒ D A 3 = D C 5
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
D A 3 = D C 5 ⇒ D A + D C 3 + 5 = A C 8 = 8 8 = 1
=> DA= 3.1 = 3; DC = 5.1 = 5
Vậy AD = 3
Đáp án: B
BT
24 tháng 10 2017
Từ D hạ các đường vuông góc DH xống AC và DK xuống AB.
Tứ giác HDKA là hình vuông vì vậy \(AH^2+HD^2=AD^2\) suy ra \(2AH^2=4^2\Leftrightarrow AH=8\)\(\Leftrightarrow AH=2\sqrt{2}\left(cm\right)\).
Suy ra \(AH=HD=DK=AK=2\sqrt{2}\left(cm\right)\).
Áp dụng định lý Pi-ta-go trong tam HCD ta có: \(HC=\sqrt{DC^2-HD^2}=\sqrt{5^2-\left(2\sqrt{2}\right)^2}=\sqrt{17}\left(cm\right)\).
Suy ra \(AC=AH+HC=2\sqrt{2}+\sqrt{17}\left(cm\right)\).
Tam giác BDI đồng dạng với tam giác BCA nên: \(\frac{BD}{BC}=\frac{BI}{BA}=\frac{DI}{CA}\).
Suy ra \(\frac{BD}{BC}=\frac{DI}{CA}\Leftrightarrow\frac{BD}{BD+5}=\frac{2\sqrt{2}}{2\sqrt{2}+\sqrt{17}}\)\(BD=\frac{10\sqrt{2}}{\sqrt{17}}=\frac{10\sqrt{34}}{17}\left(cm\right)\).
\(BC=BD+DC=\frac{10\sqrt{34}}{17}+5\) (cm).
\(BI^2=BD^2-DI^2=\left(\frac{10\sqrt{34}}{17}\right)^2-\left(2\sqrt{2}\right)^2=\frac{64}{17}\).
Suy ra \(BI=\frac{8\sqrt{17}}{17}\left(cm\right)\).
\(AB=BI+IA=\frac{8\sqrt{17}}{17}+2\sqrt{2}\left(cm\right)\).
10 tháng 12 2023
Xét ΔBAH có BI là phân giác
nên \(\dfrac{AI}{AB}=\dfrac{IH}{BH}\)
Xét ΔABC có BD là phân giác
nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)
Xét ΔABC có AD là phân giác
nên \(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos\left(\dfrac{BAC}{2}\right)\)
=>\(3=\dfrac{2\cdot\sqrt{3}\cdot AC}{\sqrt{3}+AC}\cdot cos45\)
=>\(3=\dfrac{2\sqrt{3}\cdot AC}{AC+\sqrt{3}}\cdot\dfrac{\sqrt{2}}{2}=\dfrac{\sqrt{6}\cdot AC}{AC+\sqrt{3}}\)
=>\(3AC+3\sqrt{3}=\sqrt{6}\cdot AC\)
=>\(\left(3-\sqrt{6}\right)\cdot AC=-3\sqrt{3}\)
=>\(AC=\dfrac{-3\sqrt{3}}{3-\sqrt{6}}< 0\)
=>Không có tam giác ABC nào thỏa mãn dữ kiện đề bài
=>Ko tính được góc ADB