Cho hình thang vuông ABCD vuông góc ở A và D ;AB = 6 cm,AD = 12 cm;BC =\(\frac{2}{3}\)AD.
a)Tính diện tích hình thang ABCD.
b)Kéo dài các cạnh bên AB và và DC,chúng gặp nhau tại K.Tính độ dài cạnh KB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

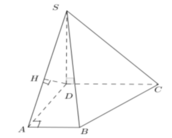
+) Vì ABCD là hình thang nên: CD // AB ⇒ CD// mp(SAB).
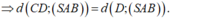
- Kẻ DH ⊥ SA.
+) Ta có:
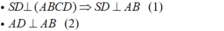
- Từ (1) và (2) suy ra:
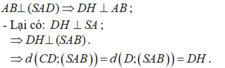
- Trong tam giác vuông SAD ta có:
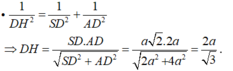

a, Áp dụng các hệ thức lượng trong tam giác vuông ABD, tính được BD = 25cm, OB = 9cm, OD = 16cm
b, Áp dụng các hệ thức lượng trong tam giác vuông DAC tính được OA = 12cm, AC = 100 3 cm
c, Tính được S = 1250 3 c m 2

Xét tam giác vuông OAB:
\(OB=\sqrt{AB^2-OA^2}=4\)
Áp dụng hệ thức lượng cho tam giác vuông ABD với đường cao AO:
\(AB^2=OB.BD\Rightarrow BD=\dfrac{AB^2}{OB}=13\)
\(\Rightarrow\left\{{}\begin{matrix}OD=BD-OB=9\\AD=\sqrt{BD^2-AB^2}=\sqrt{29}\end{matrix}\right.\)
\(\widehat{BAO}=\widehat{DCO}\left(slt\right)\Rightarrow\Delta_VAOB\sim\Delta_VCOD\) (g.g)
\(\Rightarrow\dfrac{AB}{DC}=\dfrac{OB}{OD}\Rightarrow DC=\dfrac{AB.OD}{OB}=\dfrac{9\sqrt{13}}{2}\)
\(S_{ABCD}=\dfrac{1}{2}AD.\left(AB+CD\right)=\dfrac{1}{2}.\sqrt{29}.\left(2\sqrt{13}+\dfrac{9\sqrt{13}}{2}\right)=...\)

a, Bạn chứng minh được \(\Delta ABD\infty\Delta BDC\left(g.g\right)\)
\(\Rightarrow\frac{AB}{BD}=\frac{BD}{DC}\Rightarrow AB.DC=BD^2\Rightarrow2.8=BD^2\Rightarrow BD^2=16\Rightarrow BD=4\left(cm\right)\)(vì AB = 2cm , CD = 8 cm)
Ta có: \(\frac{BD}{CD}=\frac{4}{8}=\frac{1}{2}\)
Xét tam giác BDC vuông tại B có: BD = 1/2 CD nên \(\widehat{C}=30^0\)
ABCD là hình thang vuông(gt) \(\Rightarrow AB//CD\)
\(\Rightarrow\widehat{ABC}+\widehat{C}=180^0\) ( 2 góc trong cùng phía)
\(\Rightarrow\widehat{ABC}+30^0=180^0\) (do góc C = 30 độ)
\(\Rightarrow\widehat{ABC}=150^0\)
b, Áp dụng định lí Pitago vào tam giác ABD vuông tại A, tính được: \(AD=\sqrt{12}\left(cm\right)\)
Diện tích hình thang ABCD là:
\(\frac{\left(2+8\right).\sqrt{12}}{2}=5\sqrt{12}\left(cm^2\right)\)
Chúc bạn học tốt.
Giusp mình với.Cần gấp lắm
tra mạng