câu 1
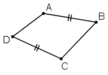
ABCD là hình bình hành; AB>AD;A>90 độ. M là trung điểm AB, N trung điểm DC. AC cắt MD tại P và BN tại Q.
C/m AP=PQ=QC
câu 2
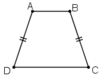
Cho tam giác ABC nhọn,AB<AC;CM,BN là trung tuyến giao nhau tại G; Q là trung điểm BG,P là trung điểm CG.
C/m MNPQ là hình bình hành

Mình gợi ý cho bạn nhé.
Câu 1:
ABCD là hình bình hành nên: AB =CD và AB song song với CD
Bạn tự chứng minh được MBND là hình bình hành vì MB= ND và MB song song với ND
Do đó: MD song song với BN hay MP song song với BQ
Xét tam giác ABQ có M là trung điểm của AB và MP song song với BQ
Suy ra: AP =PQ
Tương tự với tam giác PDC, ta cũng có: PQ =QC
Vậy AP=PQ=QC.
Câu 2:
MN là đường trung bình của tam giác ABC nên MN song song với BC và MN=1/2 BC.
PQ là đường trung bình của tam giác BCG do đó: PQ song song với BC và PQ =1/2 BC
Vậy MN song song với PQ và MN=PQ
VÌ thế MNPQ là hình bình hành (DHNB)
Chúc bạn học tốt.