Cho hàm số: y = 4x (1)
a) Vẽ đồ thị hàm số trên
b) Điểm A( 1; 4) có thuộc đồ thị hàm số (1) không? Vì sao?
c) Điểm B( -2 ; 8) có thuộc đồ thị hàm số (1) không? Vì sao?
d) Tình giá trị của hàm số khi x = - 0,5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 1 2023
b: Tọa độ giao điểm là:
2x-1=x+2 và y=x+2
=>3x=3 và y=x+2
=>x=1 và y=3
a: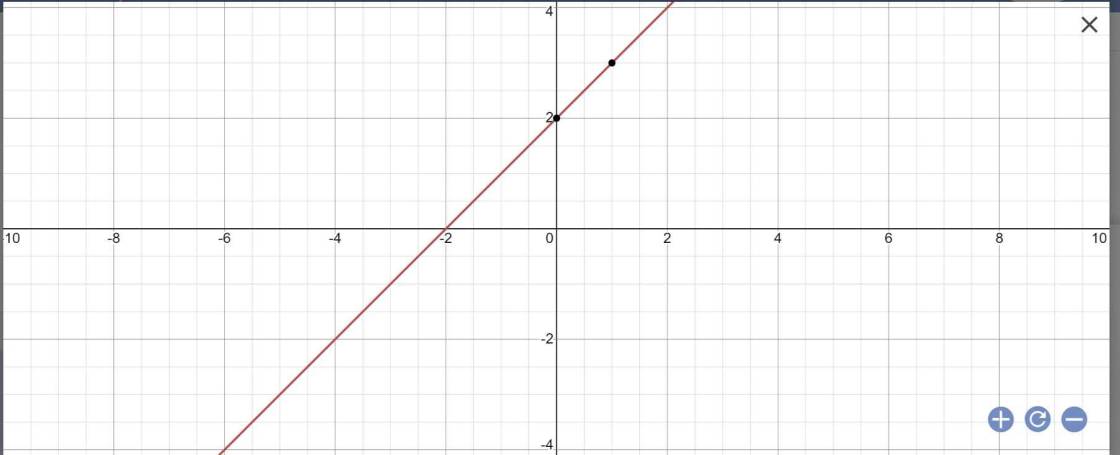 
17 tháng 2 2022
b: Thay x=a và y=6 vào hàm số, ta được:
-3/2a=6
hay a=-4
CD
5 tháng 12 2021
b, Thay điểm M vào đồ thị hàm số, ta có:
-2 = 3.-6
<=> -2 =-18 (vô lý)
Vậy điểm M ko thuộc đths y=3x
7 tháng 5 2021
a) vẽ bạn tự vẽ nha
b) Xét pt hoành độ giao điểm chung của (d) và (P) ta có:
\(\frac{1}{4}x^2=x+m\)
\(\Leftrightarrow x^2-4x-4m=0\left(1\right)\)
\(\Delta^,=4+4m\)
Để (d) tiếp xúc với (P) \(\Leftrightarrow\Delta^,=0\)
\(\Leftrightarrow4+4m=0\)
\(\Leftrightarrow m=-1\)
Thay m=-1 vào pt (1) ta được :
\(x^2-4x+4=0\)
\(\Leftrightarrow\left(x-2\right)^2=0\)
\(\Leftrightarrow x=2\)
\(\Rightarrow y=\frac{1}{4}.2^2=1\)
Gọi tọa độ tiếp điểm của (d) tiếp xúc với (P) là A(x,y)
=> tọa độ tiếp điểm là \(A\left(2;1\right)\)
14 tháng 1 2022
Bài 9:
b: Điểm A thuộc đồ thị vì \(y_A=4=-2\cdot\left(-2\right)=-2\cdot x_A\)
Bài 10:
a: Thay x=1 và y=-3 vào (d), ta được:
\(a\cdot1=-3\)
hay a=-3
15 tháng 12 2016
a.TC: y = 1/4.
Cho x=4 vao hso y=1/4x
=>y= 1/4*4=1
vay diem A(4;1) thuoc do thi ham so y=1/4x
vay do thi hso y=1/4x la đường thẳng OA.dang vay mik ve hoi xau xin loi ban nho them dong y=1/4 x tren duong thang cheo vs danh dau diem A nhe,
b)M(4;1)
Thay x=4 vào đồ thị hàm số y=1/4 x.
=> y=4*1/4=1
=. diem M co thuoc do thi hso y=1/4 x
AH
Akai Haruma
Giáo viên
6 tháng 7
Lời giải:
a. Cho $x=0$ thì $y=-4x=0$. Ta có điểm $A(0;0)$
Cho $x=1$ thì $y=-4.1=-4$. Ta có điểm $B(1;-4)$
Nối A-B ta được đths $y=-4x$
b.
$f(2)=-4.2=-8; f(-5)=-4(-5)=20$
c.
Để $A(a;6)$ thuộc đths thì $y_A=-4x_A$
$\Rightarrow 6=-4a\Rightarrow a=\frac{6}{-4}=\frac{-3}{2}$
H9
HT.Phong (9A5)
CTVHS
7 tháng 12 2023
a)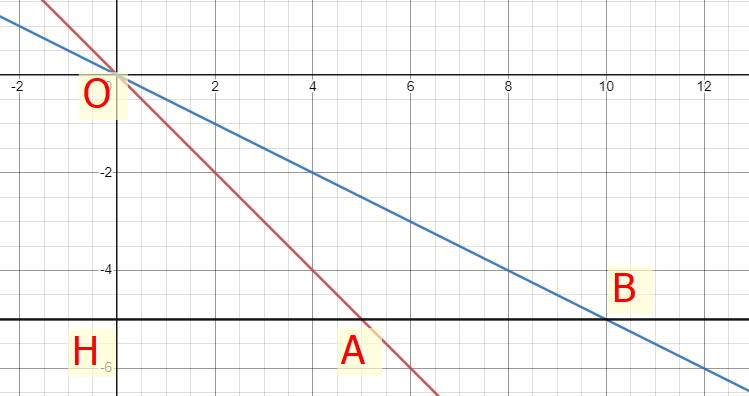 
b) Ta có đường thẳng đi qua điểm H(0;-5) nên phương trình đường thẳng đi qua H là:
\(y=0x-5\Rightarrow y=-5\)
Phương trình hoành độ giao điểm của đường thẳng \(y=-5\) và \(y=-x\) là:
\(-5=-x\)
\(\Rightarrow x=5\)
Tọa độ điểm A là (5;-5)
Phương trình hoành độ giao điểm của đường thẳng \(y=-5\) và \(y=-\dfrac{1}{2}x\) là:
\(-5=-\dfrac{1}{2}x\)
\(\Rightarrow\dfrac{1}{2}x=5\)
\(\Rightarrow x=5:\dfrac{1}{2}\)
\(\Rightarrow x=10\)
Tọa độ điểm B là (10;-5)
c) Ta có: A(5;-5) và B(10;-5)
Độ dài đường thẳng AB là \(10-5=5\left(đvđd\right)\)
Có A(5;-5) ⇒ HA = 5 (đvđd)
Xét tam giác OHA vuông tại H áp dụng định lý Py-ta-go ta có:
\(OA^2=HA^2+OH^2\) (tọa độ điểm H(0;-5) nên OH = 5 đvđd)
\(\Rightarrow OA=\sqrt{5^2+5^2}=\sqrt{50}=5\sqrt{2}\left(đvđd\right)\)
Có B(10;-5) ⇒ HB = 10 (đvđd)
Xét tam giác OHB vuông tại H áp dụng định lý Py-ta-go ta có:
\(OB^2=HB^2+OH^2\)
\(\Rightarrow OB=\sqrt{10^2+5^2}=\sqrt{125}=5\sqrt{5}\left(đvđd\right)\)
Chu vi: \(C_{OAB}=AB+OA+OB=5+5\sqrt{2}+5\sqrt{5}\approx23,25\left(đvđd\right)\)
Diện tích: \(S_{OAB}=\dfrac{1}{2}\cdot OH\cdot AB=\dfrac{1}{2}\cdot5\cdot5=12,5\left(đvdt\right)\)