Lập phương trình đường thẳng đi qua giao điểm của hai đường thẳng 2x-3y=8;5x+4y=-3 và song song với đường thẳng y=2x-1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(d): y=ax+b
Vì (d) đi qua điểm I(-1;2) nên: -a+b=2
Mà (d) vuông góc với đth: y=\(\dfrac{2}{3}x+\dfrac{7}{3}\) nên: a.\(\dfrac{2}{3}\)= -1 => a=\(\dfrac{-3}{2}\)
=> b=\(\dfrac{1}{2}\)
Do đó: (d): y=\(\dfrac{-3}{2}\)x+\(\dfrac{1}{2}\)

1, gọi phương trình đường thẳng đi qua A(1;3)là y=ax+b(d)
Vì đường thẳng (d) // đường thẳng y=x
=>a=a'=>a=1
Vì đường thẳng đi qua điểm A(1;3), ta thay x=1 và y=3 vào (d)
Ta có: 3=1.1+b
\(\Leftrightarrow b=2\)
Vậy pt đường thẳng có dạng y=x+2
2, gọi pt đường thẳng đi qua B(2;0) là y=ax+b(d)
Vì (d)⊥đường thẳng y=2x+3
=>a.a'=-1\(\Rightarrow\)a.2=-1
\(\Leftrightarrow a=\dfrac{-1}{2}\)
Đường thẳng (d) đi qua B(2;0) nên thay x=2 và y=0 vào (d)
Ta được: 0=\(\dfrac{-1}{2}\).2+b
\(\Leftrightarrow b=1\)
Vậy pt đường thẳng có dạng y=\(\dfrac{-1}{2}x+1\)

Lời giải:
$(d_1): y=2x+1$
$(d_2): y=8-\frac{x}{3}$
PT hoành độ giao điểm: $y=2x+1=8-\frac{x}{3}$
$\Rightarrow x=3; y=7$
Gọi PTĐT cần tìm có dạng $y=ax+b$
Ta có: \(\left\{\begin{matrix} 7=3a+b\\ -3=-2a+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=2\\ b=1\end{matrix}\right.\)
Vậy PTĐT cần tìm là $y=2x+1$

a: Phương trình hoành độ giao điểm là:
2x+1=x+1
=>2x-x=1-1
=>x=0
Thay x=0 vào y=x+1, ta được:
y=0+1=1
=>A(0;1)
b: Vì (d4) có hệ số góc là -4 nên (d4): y=-4x+b
Thay x=0 và y=1 vào (d4), ta được:
b-4*0=1
=>b=1
=>y=-4x+1
c: Vì (d5)//(d6) nên (d5): y=0,5x+a
Thay x=0 và y=1 vào (d5), ta được:
a+0,5*0=1
=>a=1
=>y=0,5x+1
d: Thay x=0 và y=1 vào (d3), ta được:
0*(m+1)+2m-1=1
=>2m-1=1
=>2m=2
=>m=1

Đáp án B
Từ giả thiết suy ra
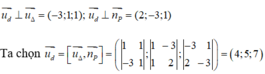
Mặt khác đường thẳng d đi qua điểm M(2;-1;1) nên phương trình tham số của đường thẳng d là: x = 2+ 4t, y = -1, + 5t, z = 1 + 7t.
Vậy đáp án đúng là B.


 và song song với mặt phẳng (P): 2x - 3y + z - 2 = 0.
và song song với mặt phẳng (P): 2x - 3y + z - 2 = 0.
Tọa độ giao của (d1) và (d2) là:
2x-3y=8 và 5x+4y=-3
=>x=1 và y=-2
Vì (d)//y=2x-1 nên a=2
=>y=2x+b
Thay x=1 và y=-2 vào (d), ta được:
b+2=-2
=>b=-4