30: Cho đường tròn (O;5cm) và OA = 6cm. Hãy cho biết vị trí của điểm A với (O;5cm)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 10 2018
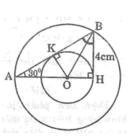
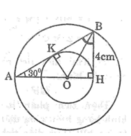Kẻ OK ⊥ AB (1)
Theo giả thiết ,OB là đường phân giác của góc B nên ta có:
OK = OH (tính chất đường phân giác) (2)
Từ (1) và (2) suy ra (O;OH) tiếp xúc với AB tại K
31 tháng 12 2023
Xét ΔOAM vuông tại A có \(tanAOM=\dfrac{AM}{OA}\)
=>\(\dfrac{AM}{9}=tan30=\dfrac{1}{\sqrt{3}}\)
=>\(AM=\dfrac{9}{\sqrt{3}}=3\sqrt{3}\left(cm\right)\)
4 tháng 9 2021
a: Xét ΔAOM vuông tại A có
\(\sin\widehat{AMO}=\dfrac{OA}{OM}\)
\(\Leftrightarrow OM=OA:\dfrac{1}{2}=2\cdot OA=2\cdot R\)
CM
15 tháng 4 2017
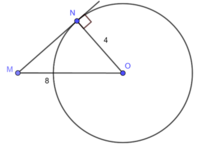
Vì MN là tiếp tuyến của đường tròn (O) tại N nên
Xét tam giác vuông MNO có:
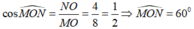
Đáp án: D
9 tháng 12 2021
a: Xét ΔOBC có OB=OC
nên ΔOBC cân tại O
mà \(\widehat{CBO}=60^0\)
nên ΔOBC đều
Xét ΔOCM có
CB là đường trung tuyến
CB=OM/2
Do đó: ΔOCM vuông tại C
hay MC là tiếp tuyến của (O)
Gọi M là giao điểm của OA và (O;5cm)
Vị trí của điểm A so với tâm O là đường tròn tâm O bán kính 6cm
Suy ra vị trí của điểm A so với (O;5cm) là tập hợp các điểm cách 1 điểm chuyển động trên đường tròn (O;5cm) 1 khoảng là 6cm - 5cm = 1cm, và sao cho O, M, A thẳng hàng.