Cho \(\overrightarrow{a}\left(1;2\right)\) và \(\overrightarrow{b}\left(3;4\right).\)Vecto \(\overrightarrow{m}=2\overrightarrow{a}+3\overrightarrow{b}\) có toạ độ là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HP
27 tháng 12 2020
\(\overrightarrow{a}\perp\overrightarrow{b}\Rightarrow\overrightarrow{a}.\overrightarrow{b}=0\)
\(\left(2\overrightarrow{a}-\overrightarrow{b}\right)\left(\overrightarrow{a}+\overrightarrow{b}\right)=2a^2+2\overrightarrow{a}.\overrightarrow{b}-\overrightarrow{a}.\overrightarrow{b}-b^2\)
\(=2a^2-b^2+\overrightarrow{a}.\overrightarrow{b}\)
\(=2.1-2+0=0\)
\(\Rightarrow\left(2\overrightarrow{a}-\overrightarrow{b}\right)\perp\left(\overrightarrow{a}+\overrightarrow{b}\right)\)
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
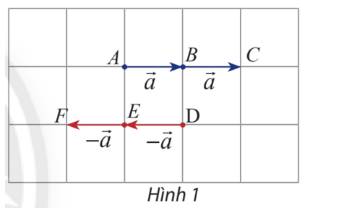
Dựa vào hình 1 ta thấy
Vectơ \(\overrightarrow a + \overrightarrow a = \overrightarrow {AC} \) có độ dài bằng 2 lần vectơ \(\overrightarrow a \)và cùng hướng với vectơ \(\overrightarrow a \)
Vectơ \(\left( { - \overrightarrow a } \right) + \left( { - \overrightarrow a } \right)= \overrightarrow {DF}\) có độ dài bằng 2 lần vectơ \(\left( { - \overrightarrow a } \right)\) và cùng hướng với vectơ \(\left( { - \overrightarrow a } \right)\)
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
a) Ta có hai vectơ \(\overrightarrow i \) và \(\overrightarrow j \) vuông góc nên \(\overrightarrow i .\overrightarrow j = 0\)
+) \({\left( {\overrightarrow i + \overrightarrow j } \right)^2} = {\left( {\overrightarrow i } \right)^2} + {\left( {\overrightarrow j } \right)^2} + 2\overrightarrow i .\overrightarrow j = {\left| {\overrightarrow i } \right|^2} + {\left| {\overrightarrow j } \right|^2} = 1 + 1 = 2\)
+) \({\left( {\overrightarrow i + \overrightarrow j } \right)^2} = {\left( {\overrightarrow i } \right)^2} + {\left( {\overrightarrow j } \right)^2} - 2\overrightarrow i .\overrightarrow j = {\left| {\overrightarrow i } \right|^2} + {\left| {\overrightarrow j } \right|^2} = 1 + 1 = 2\)
+) \(\left( {\overrightarrow i + \overrightarrow j } \right)\left( {\overrightarrow i - \overrightarrow j } \right) = {\left( {\overrightarrow i } \right)^2} - {\left( {\overrightarrow j } \right)^2} = {\left| {\overrightarrow i } \right|^2} - {\left| {\overrightarrow j } \right|^2} = 1 - 1 = 0\)
b) Sử dụng kết quả của câu a) ta có:
\(\overrightarrow a .\overrightarrow b = \left( {2\overrightarrow i + 2\overrightarrow j } \right).\left( {3\overrightarrow i - 3\overrightarrow j } \right) = 2.3.\left( {\overrightarrow i + \overrightarrow j } \right).\left( {\overrightarrow i - \overrightarrow j } \right) = 6.0 = 0\)
\(\overrightarrow a .\overrightarrow b = 0 \Rightarrow \overrightarrow a \bot \overrightarrow b \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 90^\circ \)
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 12 2020
1.
Đặt \(P=\left|\overrightarrow{AD}+3\overrightarrow{AB}\right|\Rightarrow P^2=AD^2+9AB^2+6\overrightarrow{AD}.\overrightarrow{AB}\)
\(=AD^2+9AB^2=10AB^2=10a^2\)
\(\Rightarrow P=a\sqrt{10}\)
2.
Tam giác ABC đều nên AM là trung tuyến đồng thời là đường cao \(\Rightarrow AM\perp BM\)
\(AM=\dfrac{a\sqrt{3}}{2}\) ; \(BM=\dfrac{a}{2}\)
\(T=\left|\overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|\overrightarrow{MA}+2\overrightarrow{MB}\right|\)
\(\Rightarrow T^2=MA^2+4MB^2+4\overrightarrow{MA}.\overrightarrow{MB}=MA^2+4MB^2\)
\(=\left(\dfrac{a\sqrt{3}}{2}\right)^2+4\left(\dfrac{a}{2}\right)^2=\dfrac{7a^2}{4}\Rightarrow T=\dfrac{a\sqrt{7}}{2}\)
3.
\(T=\left|\overrightarrow{AB}+\overrightarrow{CG}\right|=\left|\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CB}\right|=\left|\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{AB}\right|\)
\(=\left|\dfrac{4}{3}\overrightarrow{AB}-\dfrac{2}{3}\overrightarrow{AC}\right|\Rightarrow T^2=\dfrac{16}{9}AB^2+\dfrac{4}{9}AC^2-\dfrac{16}{9}\overrightarrow{AB}.\overrightarrow{AC}\)
\(=\dfrac{20}{9}AB^2-\dfrac{16}{9}AB^2.cos60^0=\dfrac{20}{9}a^2-\dfrac{16}{9}a^2.\dfrac{1}{2}=\dfrac{4}{3}a^2\)
\(\Rightarrow T=\dfrac{2a}{\sqrt{3}}\)
20 tháng 1 2023
(1); vecto u=2*vecto a-vecto b
=>\(\left\{{}\begin{matrix}x=2\cdot1-0=2\\y=2\cdot\left(-4\right)-2=-10\end{matrix}\right.\)
(2): vecto u=-2*vecto a+vecto b
=>\(\left\{{}\begin{matrix}x=-2\cdot\left(-7\right)+4=18\\y=-2\cdot3+1=-5\end{matrix}\right.\)
(3): vecto a=2*vecto u-5*vecto v
\(\Leftrightarrow\left\{{}\begin{matrix}a=2\cdot\left(-5\right)-5\cdot0=-10\\b=2\cdot4-5\cdot\left(-3\right)=15+8=23\end{matrix}\right.\)
(4): vecto OM=(x;y)
2 vecto OA-5 vecto OB=(-18;37)
=>x=-18; y=37
=>x+y=19
AH
Akai Haruma
Giáo viên
15 tháng 8 2021
Lời giải:
Xét hai vecto bất kỳ \(\overrightarrow{AB}, \overrightarrow{CD}\). Kẻ vecto $\overrightarrow{CT}$ sao cho $\overrightarrow{CT}=\overrightarrow{BA}$
Ta có:
\(|\overrightarrow{AB}+\overrightarrow{CD}|=|\overrightarrow{TC}+\overrightarrow{CD}|=|\overrightarrow{TD}|\)
\(|\overrightarrow{AB}|+|\overrightarrow{CD}|=|\overrightarrow{TC}|+|\overrightarrow{CD}|\)
Mà theo bđt tam giác thì:
\(|\overrightarrow{TC}+\overrightarrow{CD}|\geq |\overrightarrow{TD}|\Rightarrow |\overrightarrow{AB}|+\overrightarrow{CD}|\geq |\overrightarrow{AB}+\overrightarrow{CD}|\)
Dấu "=" xảy ra khi \(T, C,D\) thẳng hàng và $C$ nằm giữa $T,D$
$\Leftrightarrow \overrightarrow{TC}, \overrightarrow{CD}$ cùng hướng
$\Leftrightarrow \overrightarrow{AB}, \overrightarrow{CD}$ cùng hướng
Vậy với $\overrightarrow{a}, \overrightarrow{b}$ bất kỳ thì $|\overrightarrow{a}|+|\overrightarrow{b}|\geq |\overrightarrow{a}+\overrightarrow{b}|$. Dấu "=" xảy ra khi $\overrightarrow{a}, \overrightarrow{b}$ cùng hướng.
------------------
Áp dụng vào bài toán:
\(|\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}|\leq |\overrightarrow{a}+\overrightarrow{b}|+|\overrightarrow{c}|\leq |\overrightarrow{a}|+|\overrightarrow{b}|+|\overrightarrow{c}|\)
Dấu "=" xảy ra khi \(\overrightarrow{a}, \overrightarrow{b}\) cùng hướng và \(\overrightarrow{a}+\overrightarrow{b}, \overrightarrow{c}\) cùng hướng
\(\Leftrightarrow \overrightarrow{a}, \overrightarrow{b}, \overrightarrow{c}\) cùng hướng
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 12 2022
a.
Gọi G là trọng tâm tam giác ABC \(\Rightarrow\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
\(\Rightarrow T=\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\right|\)
\(=\left|3\overrightarrow{MG}\right|=3\left|\overrightarrow{MG}\right|\)
\(\Rightarrow T_{min}\) khi và chỉ khi \(MG_{min}\Rightarrow MG=0\) hay M trùng G
Theo công thức trọng tâm: \(\left\{{}\begin{matrix}x_M=\dfrac{2-1+6}{3}=\dfrac{7}{3}\\y_M=\dfrac{3-1+0}{3}=\dfrac{2}{3}\end{matrix}\right.\) \(\Rightarrow M\left(\dfrac{7}{3};\dfrac{2}{3}\right)\)
b.
Tương tự câu a, ta có \(T=3\left|\overrightarrow{MG}\right|\) đạt min khi MG đạt min
\(\Rightarrow\) M là hình chiếu vuông góc của G lên Ox
Mà \(G\left(\dfrac{7}{3};\dfrac{2}{3}\right)\Rightarrow M\left(\dfrac{7}{3};0\right)\)
c.
Do M thuộc Ox nên tọa độ có dạng: \(M\left(m;0\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}=\left(2-m;3\right)\\\overrightarrow{MB}=\left(-1-m;-1\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{u}=\left(3m+6;7\right)\)
\(\Rightarrow\left|\overrightarrow{u}\right|=\sqrt{\left(3m+6\right)^2+7^2}\ge\sqrt{0+7^2}=7\)
Dấu "=" xảy ra khi \(3m+6=0\Rightarrow m=-2\)
\(\Rightarrow M\left(-2;0\right)\)
BT
16 tháng 5 2017
\(\overrightarrow{x}=\overrightarrow{a}+\overrightarrow{b}=\left(1+0;-2+3\right)=\left(1;1\right)\).
\(\overrightarrow{y}=\overrightarrow{a}-\overrightarrow{b}=\left(0-1;3-\left(-2\right)\right)=\left(-1;5\right)\).
\(\overrightarrow{z}=3\overrightarrow{a}-4\overrightarrow{b}=3\left(1;-2\right)-4\left(0;3\right)=\left(3;-6\right)-\left(0;12\right)\)\(=\left(3;-18\right)\).
\(\overrightarrow{m}=2\left(1;2\right)+3\left(3;4\right)=\left(2;4\right)+\left(9;12\right)=\left(11;16\right)\)