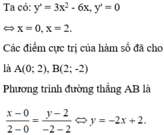Viết phương trình đường thẳng đi qua điểm (3;4) và tiếp xúc với đồ thị hàm số \(y=\frac{1}{2}x^2\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
24 tháng 11 2019
Đáp án A
Ta có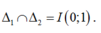 
Vì A thuộc ∆1 nên A( a; a+ 1).
Vì P( 2;1) là trung điểm của đoạn AB nên B( 4-a; 1-a).
Mặt khác:
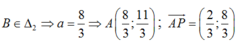
Đường thẳng AP có VTPT ( 4;-1) và qua P(2;1) nên có phương trình:
4x – y- 7 = 0
HP
4 tháng 5 2021
b, \(d\left(I;\Delta\right)=R\Leftrightarrow\dfrac{\left|-2+6+m\right|}{\sqrt{13}}=\sqrt{13}\)
\(\Rightarrow\left[{}\begin{matrix}m=9\\m=-17\end{matrix}\right.\)
HP
4 tháng 5 2021
c, Dễ tìm được tọa độ A, B: \(\left\{{}\begin{matrix}A=\left(-3,-1\right)\\B=\left(2,0\right)\end{matrix}\right.\)
Phương trình tiếp tuyến tại A có dạng: \(\Delta_1:ax+by+3a+b=0\left(a^2+b^2\ne0\right)\)
Ta có: \(d\left(I,\Delta_1\right)=\dfrac{\left|-a+2b+3a+b\right|}{\sqrt{a^2+b^2}}=\sqrt{13}\)
\(\Leftrightarrow\left(2a+3b\right)^2=13a^2+13b^2\)
\(\Leftrightarrow4a^2+9b^2+12ab=13a^2+13b^2\)
\(\Leftrightarrow9a^2+4b^2-12ab=0\)
\(\Leftrightarrow9a^2+4b^2-12ab=0\)
\(\Leftrightarrow3a=2b\)
\(\Rightarrow\Delta_1:2x+3y+9=0\)
Tương tự tiếp tuyến tại B: \(\Delta_2:3x-2y-6=0\)
16 tháng 2 2021
Phương trình đườn thẳng (d) sẽ có dạng là: (d): y=ax+b(a≠0)
Ta có: 2x-y+3=0
\(\Leftrightarrow-y+2x+3=0\)
\(\Leftrightarrow-y=-2x-3\)
\(\Leftrightarrow y=2x+3\)
Vì (d) có cùng hệ số góc với đường thẳng 2x-y+3=0 nên a=2
hay (d): y=2x+b
Vì (d) đi qua A(-2;3) nên Thay x=-2 và y=3 vào hàm số y=2x+b, ta được:
\(2\cdot\left(-2\right)+b=3\)
\(\Leftrightarrow b-4=3\)
hay b=7
Vậy: (d): y=2x+7
6 tháng 12 2021
b: Vì (d')//(d) nên a=2
Vậy: (d'): y=2x+b
Thay x=2 và y=3 vào (d'), ta được:
b+4=3
hay b=-1
