Cho hàm số f(x) liên tục trên đoạn [1;3] và có bảng biến thiên như sau:
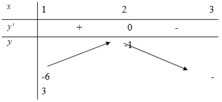
Tổng tất cả các số nguyên m để phương trình f ( x - 1 ) = m x 2 - 6 x + 12 có hai nghiệm phân biệt trên đoạn [2;4] bằng
A. -75
B. -72
C. -294
D. -297
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp: Sử dụng phương pháp đổi biến, đặt t = u(x)
Cách giải:
Đặt
![]()
Đổi cận 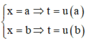
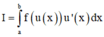


Ta có
![]()
![]()
![]()
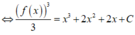
![]()
Ta có: f ( 0 ) = 1 ⇒ 1 = 3 C
![]()
![]()
Xét hàm ![]() trên [-2;1]
trên [-2;1]
Ta có
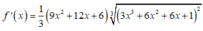
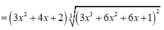
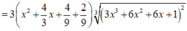
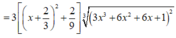
Nhận thấy f ' ( x ) > 0 ∀ x ∈ ℝ ⇒ Hàm số đồng biến trên (-2;1)
Suy ra m a x - 2 ; 1 f ( x ) = f ( 1 ) = 16 3
Chọn đáp án C.

Chọn A.
Ta có ∫ 1 4 f ' ( x ) d x = f ( 4 ) - f ( 1 ) ⇒ f ( 4 ) = f ( 1 ) + 17 = 29

Chọn B.
Ta có: D = (-∞; -2] ∪ [2; +∞).
![]() .và f(2) = 0.
.và f(2) = 0.
Vậy hàm số liên tục tại x = 2.
Với -2 < x < 2 thì hàm số không xác định.
Phương trình tương đương với:
m = g ( x ) = x 2 - 6 x + 12 f ( x - 1 ) .
Ta có
g ' ( x ) = 2 x - 6 f ( x - 1 ) + x 2 - 6 x + 12 f ' ( x - 1 )
+) Nếu 2 ≤ x < 3
⇒ g ' ( x ) > 0
+) Nếu x=3
+) Nếu 3 < x ≤ 4
⇒ g ' ( x ) < 0 .
Vậy trên đoạn [2;4] ta có g'(x)=0 ↔ x=3.
Bảng biến thiên:
Vậy phương trình có hai nghiệm phân biệt trên đoạn
2 ; 4 ⇔ - 12 < m < 3 ⇒ m ∈ - 12 , . . . , - 4 .
Tổng các số nguyên cần tìm bằng ∑ k = - 12 - 4 k = - 72
Chọn đáp án B.