Giả sử phương trình bậc hai \(ax^2+bx+c=0\) có hai nghiệm thuộc [0;3]. Tìm GTLN và GTNN của biểu thức:
\(Q=\dfrac{18a^2-9ab+b^2}{9a^2-3ab+ac}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 2: Theo định lý Vi-et ta có \(\hept{\begin{cases}x_1+x_2=-a\\x_1x_2=b\end{cases}}\)Bất Đẳng Thức cần chứng minh có dạng
\(\frac{x_1}{1+x_1}+\frac{x_2}{1+x_2}\ge\frac{2\sqrt{x_1x_2}}{1+\sqrt{x_1x_2}}\)Hay \(\frac{x_1}{1+x_2}+1+\frac{x_2}{1+x_1}+1\ge\frac{2\sqrt{x_1x_2}}{1+\sqrt{x_1x_2}}+2\)
\(\left(x_1+x_2+1\right)\left(\frac{1}{1+x_1}+\frac{1}{1+x_2}\right)\ge\frac{2\left(1+2\sqrt{x_1x_2}\right)}{1+\sqrt{x_1x_2}}\)Theo Bất Đẳng Thức Cosi ta có
\(x_1+x_2+1\ge2\sqrt{x_1x_2}+1\)Để chứng minh (*) ta quy về chứng minh
\(\frac{1}{1+x_1}+\frac{1}{1+x_2}\ge\frac{2}{1+\sqrt{x_1x_2}}\)với \(x_1;x_2>1\). Quy đồng rồi rút gọn Bất Đẳng Thức trên tương đương với
\(\left(\sqrt{x_1x_2}-1\right)\left(\sqrt{x_1}-\sqrt{x_2}\right)^2\ge0\)(Điều này hiển nhiên đúng)
Dấu "=" xảy ra khi và chỉ khi \(x_1=x_2\Leftrightarrow a^2=4b\)

Theo Vi et ta có: \(\hept{\begin{cases}x_1+x_2=\frac{-b}{a}\\x_1x_2=\frac{c}{a}\end{cases}}\)
Theo giả thuyết thì:
\(x_1^2+x_2^2=2x_1x_2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=0\)
\(\Leftrightarrow\frac{b^2}{a^2}-\frac{4c}{a}=0\)
\(\Leftrightarrow b^2-4ac=0\)
Vậy ta có ĐPCM

Giả sử x 1 , x 2 là hai nghiệm của phương trình bậc hai a x 2 + bx + c = 0 có ∆’ = 0
Do đó, phương trình có nghiệm kép 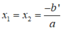
Chọn B

Đáp án: A
Bước 1 sai vì giả sử phản chứng sai, phải giả sử phương trình vô nghiệm và a, c trái dấu.

Áp dụng hệ thức Vi-ét ta có:
y1+y2= 3x1+3x2=3(x1+x2)
=\(\dfrac{-3b}{a}\)
y1y2=\(\dfrac{9c}{a}\)
Ta có pt x^2 +\(\dfrac{3b}{a}x+\dfrac{9c}{a}=0\)

gọi x1,x2 là hai nghiệm \(\Rightarrow x_1+x_2=-a\) và \(x_1x_2=b+1\)
Ta có : \(a^2+b^2=\left[-\left(x_1+x_2\right)\right]^2+\left(x_1x_2-1\right)^2\)
\(\Rightarrow a^2+b^2=\left(x_1^2+x_2^2+2x_1x_2\right)+\left(x_1^2x_2^2-2x_1x_2+1\right)\)
\(\Rightarrow a^2+b^2=x_1^2+x_2^2+x_1^2x_2^2+1=\left(x_1^2+1\right)\left(x_2^2+1\right)\)là hợp số

đoạn sau là x2-ax-1/(2a2)=0 nha, viết thiếu.
@nguyenthanhtuan cái này là chứng minh mà bạn.
Tham khảo:
Câu hỏi của Nguyễn Ngọc Ánh - Toán lớp 10 | Học trực tuyến