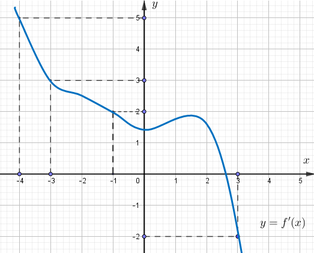
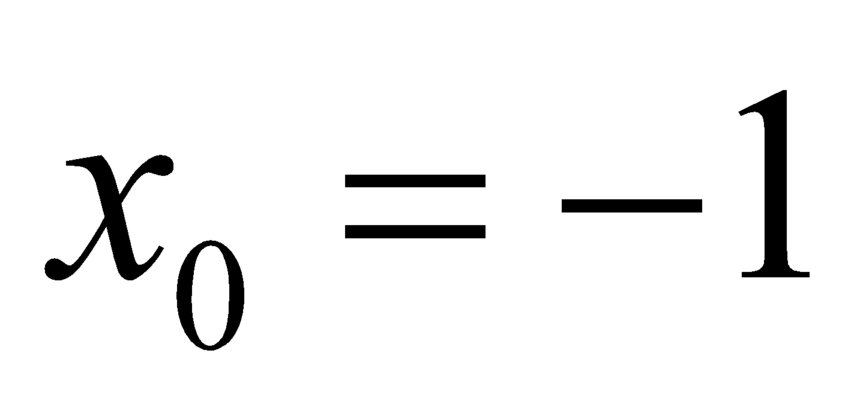Cho hàm số f(x). Biết hàm số y=f '(x) có đồ thị như hình bên. Trên đoạn [-4;3], hàm số g ( x ) = 2 f ( x ) + ( 1 - x ) 2 đạt giá trị nhỏ nhất tại điểm
A.![]() .
.
B.![]() .
.
C.![]() .
.
D.![]() .
.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Ta có ![]()
![]()
Vẽ đường thẳng y = 1-x trên cùng hệ trục chứa đồ thị y = f'(x)
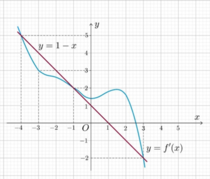
Dựa vào hình vẽ ta có g'(x) = 0 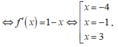
Ta có bảng biến thiên
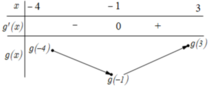
Vậy hàm số g(x) = 2f(x) + 1 - x 2 đạt giá trị nhỏ nhất tại x 0 = -1

Đáp án B
Ta có g x = 2 f x + 1 - x 2 → g ' x = 2 f ' x - 2 1 - x ; g ' x = 0 ⇔ f ' x = 1 - x
Đồ thị hàm số y = f '(x) cắt đường thẳng y = 1 - x tại x = -4, x = -1, x = -2
Đồng thời g '(x) đổi dấu từ - sang + khi đi qua x = - 1 → m i n - 4 ; 3 g x = g - 1 .

Đáp án D.
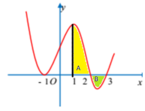
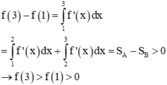
Đồ thị hàm số y = f(x) có dạng:
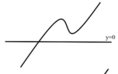
Đồ thị hàm số y = |f(x)| có dạng:
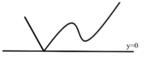
→ Hàm số y = |f(x)| có 3 điểm cực trị.

Chọn A
+ Từ đồ thị của đạo hàm ta lập được bảng biến thiên như sau
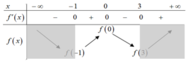
+ Dựa vào BBT ta suy ra giá trị lớn nhất của hàm số trên đoạn [-1;3] là f(0)
Chọn B
Ta có
Dựa vào hình vẽ ta có: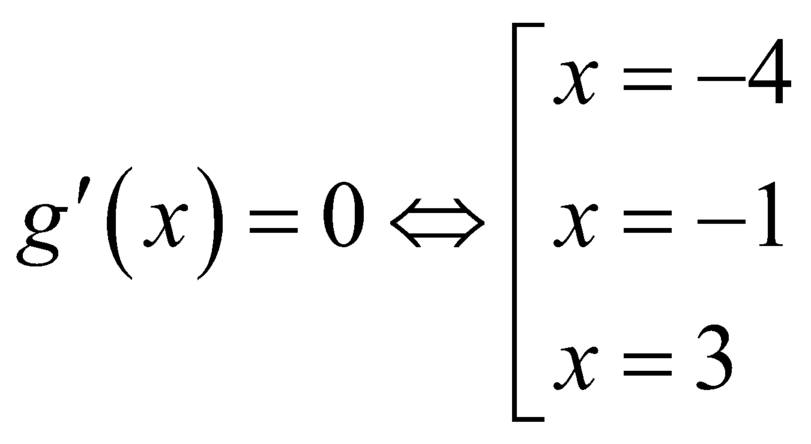 .
.
Và ta có bảng biến thiên
Suy ra hàm số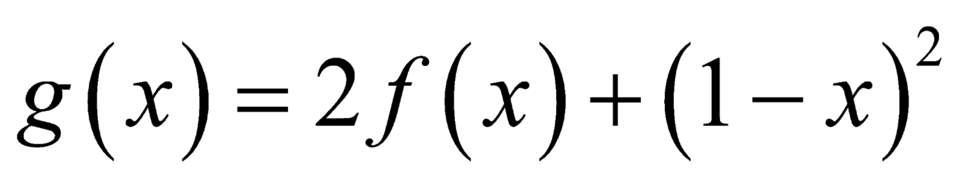 đạt giá trị nhỏ nhất tại điểm
đạt giá trị nhỏ nhất tại điểm