Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta có: ![]()
Từ điểm D kẻ đường thẳng song song với AC, cắt cạnh AB tại điểm E. Từ D kẻ đường thẳng song song với AB cắt cạnh AC tại F. Do AD là đường phân giác trong của tam giác ABC nên ta suy ra AEDF là hình thoi.
Đặt AE=AF=k. Ta có:
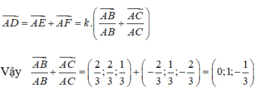
là một vectơ chỉ phương của đường thẳng AD. Từ đó suy ra C là khẳng định đúng.
Ta cũng lưu ý rằng khẳng định A sai, do tam giác ABC không cân tại đỉnh A.

Câu 1:
Chú ý độ dài 3 cạnh của tam giác là sai thì \(a+b=7=c\)
Nếu là cạnh của tam giác thì: \(\left\{{}\begin{matrix}a+b>c\\a+c>b\\c+b>a\end{matrix}\right.\)
Câu 2: Ta có:
\(m_a=\sqrt{\dfrac{b^2+c^2}{2}-\dfrac{a^2}{4}}=\sqrt{\dfrac{AC^2+AB^2}{2}-\dfrac{BC^2}{4}}\)
\(\Rightarrow m_a=\sqrt{\dfrac{9^2+4^2}{2}-\dfrac{6^2}{4}}\)
\(\Rightarrow m_a\approx6,3\)
Ta có: \(p=\dfrac{AB+AC+BC}{2}=\dfrac{4+6+9}{2}=\dfrac{19}{2}\)
\(\Rightarrow S_{ABC}=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}=\sqrt{\dfrac{19}{2}\cdot\left(\dfrac{19}{2}-6\right)\cdot\left(\dfrac{19}{2}-9\right)\cdot\left(\dfrac{19}{2}-4\right)}\approx9,5\)
\(\Rightarrow h_b=2\cdot\dfrac{S_{ABC}}{b}\Rightarrow h_b=2\cdot\dfrac{9,5}{9}\approx2,1\)

Ta có: a2 + b2 = c2 nên tam giác ABC là tam giác vuông.
Chọn C

a: A(3;1); B(2;6); C(4;-1)
\(AB=\sqrt{\left(2-3\right)^2+\left(6-1\right)^2}=\sqrt{5^2+1^2}=\sqrt{26}\)
\(AC=\sqrt{\left(4-3\right)^2+\left(-1-1\right)^2}=\sqrt{2^2+1^2}=\sqrt{5}\)
\(BC=\sqrt{\left(4-2\right)^2+\left(-1-6\right)^2}=\sqrt{2^2+7^2}=\sqrt{53}\)
Chu vi tam giác ABC là:
\(C_{ABC}=\sqrt{26}+\sqrt{5}+\sqrt{53}\left(đvđd\right)\)
b: Xét ΔABC có
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{26+5-53}{2\cdot\sqrt{26\cdot5}}\simeq-0,96\)
=>\(\widehat{A}\simeq165^0\)
c: Gọi H(x,y) là trực tâm của ΔABC
\(\overrightarrow{AH}=\left(x-3;y-1\right)\)
\(\overrightarrow{BH}=\left(x-2;y-6\right)\)
\(\overrightarrow{BC}=\left(2;-7\right);\overrightarrow{AC}=\left(1;-2\right)\)
H là trực tâm nên ta có: AH\(\perp\)BC và BH\(\perp\)AC
=>\(\left\{{}\begin{matrix}\overrightarrow{AH}\cdot\overrightarrow{BC}=0\\\overrightarrow{BH}\cdot\overrightarrow{AC}=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2\left(x-3\right)+\left(-7\right)\left(y-1\right)=0\\1\left(x-2\right)+\left(-2\right)\left(y-6\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-6-7y+7=0\\x-2-2y+12=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-7y=-1\\x-2y=-10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-7y=-1\\2x-4y=-20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3y=-1+20=19\\x-2y=-10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=-\dfrac{19}{3}\\x=-10+2y=-10-\dfrac{38}{3}=-\dfrac{68}{3}\end{matrix}\right.\)

bài 2:
ta có: AB<AC<BC(Vì 3cm<4cm<5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
bài 2:
ta có: AB <AC <BC (Vì 3cm <4cm <5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
HT mik làm giống bạn Dương Mạnh Quyết

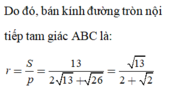
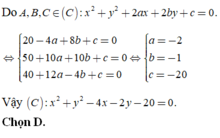
Tọa độ A là nghiệm: \(\left\{{}\begin{matrix}x+2y-5=0\\4x+13y-10=0\end{matrix}\right.\) \(\Rightarrow A\left(9;-2\right)\)
\(\Rightarrow\overrightarrow{AC}=\left(-5;5\right)=5\left(-1;1\right)\)
Phương trình AC: \(1\left(x-4\right)+1\left(y-3\right)=0\Leftrightarrow x+y-7=0\)
Phương trình đường thẳng qua C vuông góc AD có dạng:
\(2\left(x-4\right)-1\left(y-3\right)=0\Leftrightarrow2x-y-5=0\)
Gọi E là hình chiếu của C lên AD \(\Rightarrow\left\{{}\begin{matrix}2x-y-5=0\\x+2y-5=0\end{matrix}\right.\) \(\Rightarrow E\left(3;1\right)\)
Gọi F là điểm đối xứng C qua AD \(\Rightarrow F\) thuộc AB đồng thời E là trung điểm CF \(\Rightarrow F\left(2;-1\right)\)
\(\overrightarrow{AF}=\left(-7;1\right)\Rightarrow\) pt AB: \(1\left(x-2\right)+7\left(y+1\right)=0\Leftrightarrow x+7y+5=0\)
Tọa độ B có dạng: \(B\left(-7b-5;b\right)\) \(\Rightarrow M\left(\dfrac{-7b-1}{2};\dfrac{b+3}{2}\right)\)
M thuộc AM nên: \(4\left(\dfrac{-7b-1}{2}\right)+13\left(\dfrac{b+3}{2}\right)-10=0\Rightarrow b=1\Rightarrow B\left(-12;1\right)\)
\(\Rightarrow\overrightarrow{BC}\Rightarrow\) phương trình BC
Tính độ dài 3 cạnh, tính diện tích theo công thức Hê-rông
Bạn tự hoàn thành phần còn lại nhé