có bao nhiêu giá trị nguyên của tham số \(m\in\left(-2018;2018\right)\) để hàm số \(y=\sqrt{4x-12m}\) xác định trên \(\left(0;+\infty\right)\)
A. 2017 B. 2018 C. 2019 D. 2022
Chọn đáp án đúng, giải thích ngắn gọn hộ mk đc ko ạ. mk cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm số bậc nhất đồng biến suy ra a > 0 hay m > 2
m thuộc đoạn [-2018; 2018] suy ra m thuộc {3; 4; ...; 2018}
Vậy có 2016 giá trị nguyên của m cần tìm.
Chọn D.

\(y'=\dfrac{x-m-x+1}{\left(x-m\right)^2}=\dfrac{1-m}{\left(x-m\right)^2}\)
Hàm số nghịch biến trên khoảng \(\left(-\infty;2\right)\Leftrightarrow y'< 0\forall x\in\left(-\infty;2\right)\Leftrightarrow\left\{{}\begin{matrix}1-m< 0\\x\ne m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>1\\m\ge2\end{matrix}\right.\Rightarrow m\ge2\)
Có 19-2+1=18 giá trị nguyên của m thỏa mãn

b, \(\left\{{}\begin{matrix}x^2-2x-3\le0\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1\le x\le3\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)
Yêu cầu bài toán thỏa mãn khi phương trình \(f\left(x\right)=x^2-2mx+m^2-9\ge0\) có nghiệm \(x\in\left[-1;3\right]\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=m^2-m^2+9=9>0,\forall m\\-1< m< 3\\f\left(-1\right)=m^2+2m-8\ge0\\f\left(3\right)=m^2-6m\ge0\end{matrix}\right.\)
\(\Leftrightarrow m\in[2;3)\cup(-1;0]\)

https://video.vietjack.com/upload2/quiz_source1/2020/01/100-bai-trac-nghiem-ham-so-mu-va-logarit-co-loi-giai-chi-tiet-3-1-1579254891.PNG
bạn tham khảo nha

Vì hàm f(x) đã cho có 3 điểm cực trị nên f x + 2018 + m 2 cũng luôn có 3 điểm cực trị (do phép tịnh tiến không làm ảnh hưởng đến số cực trị).
Do đó ycbt ⇔ số giao điểm của đồ thị f x + 2018 + m 2 với trục hoành là 2
Để số giao điểm của đồ thị f x + 2018 + m 2 với trục hoành là 2 ta cần
• Tịnh tiến đồ thị f(x) xuống dưới tối thiểu 2 đơn vị ![]()
• Hoặc tịnh tiến đồ thị f(x) lên trên tối thiểu 2 đơn vị nhưng phải nhỏ hơn 6 đơn vị
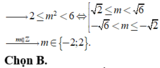
Lời giải:
Để $y=\sqrt{4x-12m}$ xác định trên $(0;+\infty)$ thì $4x\geq 12m$ với mọi $x\in (0;+\infty)$
$\Leftrightarrow m\leq \frac{x}{3}$ với mọi $x\in (0;+\infty)$
Hay $m\leq 0$
Với $m$ nguyên và $m\in (-2018;2018)$ thì $m\in\left\{-2017; 2016;...;0\right\}$
Do đó có 2018 giá trị nguyên của $m$ thỏa mãn đề bài
Đáp án B.