Viết các số chính phương liên tiếp \(1^2;2^2;3^2;.....;2012^2\) liền nhau ta được số D = 1491625.........4048144
a) Tìm số chữ số của D
b) Tìm số dư trong phép chia D cho 9
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2.
Gọi x;x+1;x+2;x+3 là 4 số tự nhiên liên tiếp ( x\(\in\) N)
Ta có : x (x+1) (x+2 ) (x+3 ) +1
=( x2 + 3x ) (x2 + 2x + x +2 ) +1
= ( x2 + 3x ) (x2 +3x + 2 ) +1 (*)
Đặt t = x2 + 3x thì (* ) = t ( t+2 ) + 1= t2 + 2t +1 = (t+1)2 = (x2 + 3x + 1 )2
=> x (x+1) (x+2 ) (x+3 ) +1 là số chính phương
hay tích 4 số tự nhiên liên tiếp cộng 1 là số chính phương
Gọi x;x+1;x+2;x+3 là 4 số tự nhiên liên tiếp ( x
∈
∈ N)
Ta có : x (x+1) (x+2 ) (x+3 ) +1
=( x2 + 3x ) (x2 + 2x + x +2 ) +1
= ( x2 + 3x ) (x2 +3x + 2 ) +1 (*)
Đặt t = x2 + 3x thì (* ) = t ( t+2 ) + 1= t2 + 2t +1 = (t+1)2 = (x2 + 3x + 1 )2
=> x (x+1) (x+2 ) (x+3 ) +1 là số chính phương
hay tích 4 số tự nhiên liên tiếp cộng 1 là số chính phương

a) Từ giả thiếtta có thể đặt : \(n^2-1=3m\left(m+1\right)\) với m là 1 số nguyên dương
Biến đổi phương trình ta có :
\(\left(2n-1;2n+1\right)=1\) nên dẫn đến :
\(TH1:2n-1=3u^2;2n+1=v^2\)
\(TH2:2n-1=u^2;2n+1=3v^2\)
\(TH1:\)
\(\Rightarrow v^2-3u^2=2\)
\(\Rightarrow v^2=2\left(mod3\right)\)
Còn lại TH2 cho ta \(2n-1\) là số chính phương
b) Ta có :
\(\frac{n^2-1}{3}=k\left(k+1\right)\left(k\in N\right)\)
\(\Leftrightarrow n^2=3k^2+3k+1\)
\(\Leftrightarrow4n^2-1=12k^2+12k+3\)
\(\Leftrightarrow\left(2n-1\right)\left(2n+1\right)=3\left(2k+1\right)^2\)
- Xét 2 trường hợp :
\(TH1:\Rightarrow\hept{\begin{cases}2n-1=3p^2\\2n+1=3q\end{cases}}\)
\(TH2:\Rightarrow\hept{\begin{cases}2n-1=p^2\\2n+1=3q^2\end{cases}}\)
+) TH1 :
Hệ \(PT\Leftrightarrow q^2=3p^2+2=2\left(mod3\right)\) ( loại, vì số chính phương chia 3 dư 0 hoặc 1 )
+) TH2 :
Hệ \(PT\Leftrightarrow p=2a+1\Rightarrow2n=\left(2a+1\right)^2+1\Rightarrow n^2=a^2+\left(a+1\right)^2\) ( dpcm )

Giả sử 1^3+2^3+...+n^3=(1+2+...+n)^2(1)
Khi n=1 thì ta sẽ có 1^3=1^2(đúng)
Giả sử (1) đúng khi n=k
Khi n=2 thì ta sẽ có 1^3+2^3=9=(1+2)^2
Ta sẽ cần chứng minh (1) đúng khi n=k+1
1^3+2^3+...+n^3
=1^3+2^3+...+k^3+(k+1)^3
=(1+2+3+...+k)^2+(k+1)^3
Xét biểu thức (k+1)^2+2(k+1)(1+2+...+k)
=(k+1)^2+2*(k+1)*k*(k+1)/2
=(k+1)^2*(1+k)=(k+1)^3
=>1^3+2^3+...+(k+1)^3
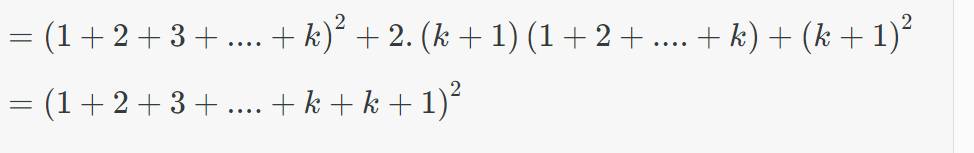
=>ĐPCM
a) Chia dãy các số chính phương thành các nhóm sau
(12; 22; 32) ; (42; 52; ...; 92); (102; 112; ...; 312); (322; ....; 992); (1002; ...; 3162); (3172; ....; 9992); (10002; ...; 20122)
Nhận xét :
- Nhóm 1 có 3 số có 1 chữ số
- Nhóm 2 gồm các số chính phương lớn hơn 32 = 9 và nhỏ hơn 102 = 100 => là các số có 2 chữ số
=> Nhóm 2 có (9 - 4 + 1) = 6 số có 2 chữ số
- Nhóm 3 gồm các số chính phương lớn hơn 92 = 81 và nhỏ hơn 322 = 1024 => là các số có 3 chữ số
=> Nhóm 3 có (31 - 10 +1) = 22 số có 3 chữ số
Tương tự,
- Nhóm 4 có 68 số có 4 chữ số
- Nhóm 5 có 217 số có 5 chữ số
- Nhóm 6 có 683 số có 6 chữ số
- Nhóm 7 có 1013 số có 7 chữ số
Vậy Số các chữ số của D là: 3.1 + 6.2 + 22.3 + 68.4 + 217.5 + 683.6 + 1013.7 = 12 627 chữ số
Xin lỗi cậu nha Qúy mình không có biết làm bài này.Xin lỗi nha