cho tam giác ABC có M,N,P lần lượt trung điểm của AB,AC,BC, G là trọng tâm của tam giác
a, tìm ảnh của tam giác AMN qua V(A;2)
b, tìm ảnh của tam giác ABC qua V(G,1/2)
c,tìm điểm E sao cho C = V(A;-2 (E)
d, tìm điểm D sao cho C = V(B;2) (D)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bạn tự vẽ hình nhé !
Nối EN, NM, ME. Ta có G là trọng tâm tam giác ABC nên G là giao điểm 3 đường trung tuyến , do đó E, G , C thẳng hàng.(1)
bây giờ chứng minh E,G,D thẳng hàng thì sẽ có C,G,E,D thẳng hàng.
Ta có E là trung điểm AB, N là trung điểm AC suy ra EN là đường trug bình tam giác ABC nên EN =1/2 BC và EN song2 với BC. lại có MC=1/2 BC ( M trug điểm BC)
suy ra EN = CM và EN song2 với CM từ đó ENCM là hình bình hành.
Xét hình bình hành ENCM có D là trung điểm MN suy ra D là trug điểm EC => ED=DC.
Vì G là trọng tâm tam giác ABC nên EG=1/3 EC=2/3ED (vì ED=1/2 EC)
Xét tam gác ENM có ED là trung tuyến , EG=2/3 ED suy ra G là trọng âm tam giác ENM. suy ra EGD thẳng hàng (2)
TỪ 1 và 2 suy ra E,G,D,C thẳng hàng

Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/2=CD/3=(BD+CD)/(2+3)=15/5=3
=>BD=6cm và CD=9cm
Xét ΔBAD có BI là phân giác
nên AI/ID=AB/BD=2
=>AI/AD=2/3=AG/AM
=>IG//BC

Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/2=CD/3=(BD+CD)/(2+3)=15/5=3
=>BD=6cm và CD=9cm
Xét ΔBAD có BI là phân giác
nên AI/ID=AB/BD=2
=>AI/AD=2/3=AG/AM
=>IG//BC

Đáp án B
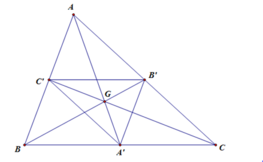
G A → = − 2 G A ' → ⇒ V G , − 2 A ' = A G B → = − 2 G B ' → ⇒ V G , − 2 B ' = B G C → = − 2 G C ' → ⇒ V G , − 2 C ' = C ⇒ V G , − 2 Δ A ' B ' C ' = Δ A B C