Cho 2 điểm A(-1;3) và B(2;2) và đường thẳng (∆): x+3y-5=0
Tìm trên ∆ điểm :
1) C sao cho ∆ABC cân tại C
2) D sao cho ∆ABD vuông tại A
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 9 2019
a/ Gọi \(D\left(a;0\right)\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-9;3\right)\\\overrightarrow{AD}=\left(a-6;-3\right)\end{matrix}\right.\)
Do A; B; D thẳng hàng \(\Leftrightarrow\frac{a-6}{-9}=\frac{-3}{3}\Rightarrow a=15\) \(\Rightarrow D\left(15;0\right)\)
b/ \(\overrightarrow{AB}=\left(-1;5\right);\) \(\overrightarrow{AD}=\left(-2;10\right)\)
\(\Rightarrow\overrightarrow{AD}=2\overrightarrow{AB}\Rightarrow A,B,D\) thẳng hàng
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 11 2019
\(\overrightarrow{AB}=\left(6;3\right)\) ; \(\overrightarrow{AC}=\left(5;-3\right)\)
Ta có \(\frac{5}{6}\ne\frac{-3}{3}\Rightarrow\overrightarrow{AB}\) và \(\overrightarrow{AC}\) ko cùng phương nên A;B;C ko thẳng hàng
\(\Rightarrow\) A;B;C là 3 đỉnh của 1 tam giác
2/ Gọi \(I\left(x;0\right)\Rightarrow\overrightarrow{AI}=\left(x+4;-1\right)\)
Để A;B;I thẳng hàng \(\Rightarrow\frac{x+4}{6}=-\frac{1}{3}\Rightarrow x+4=-2\Rightarrow x=-6\)
\(\Rightarrow I\left(-6;0\right)\)
CM
16 tháng 8 2019
Gọi (Q) và (R) theo thứ tự là mặt phẳng trung trực của AB và BC.
Những điểm cách đều ba điểm A, B, C là giao tuyến ∆ = (Q) ∩ (R).
(Q) đi qua trung điểm E(3/2; 1/2; 1) của AB và có n Q → = AB→ (1; -3; 0) do đó phương trình của (Q) là: x - 3/2 - 3(y - 1/2) = 0 hay x - 3y = 0
(R) đi qua trung điểm F(1; 1; 1) của BC và có n R → = BC → = (-2; 4; 0) do đó phương trình (R) là: x - 2y + 1 = 0
Ta có: n Q → ∧ n R → = (0; 0; -2).
Lấy D(-3; -1; 0) thuộc (Q) ∩ (R)
Suy ra ∆ là đường thẳng đi qua D và có vectơ chỉ phương u → (0; 0; 1)
nên có phương trình là: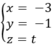 
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
a) Ta có: \(\overrightarrow {AB} = \left( {2;4} \right),\overrightarrow {AG} = \left( {2;1} \right)\)
Do \(\overrightarrow {AB} \ne k.\overrightarrow {AG} \) nên A, B, G không thẳng hàng
b) Giả sử C có tọa độ là: \(C\left( {{x_C};{y_C}} \right)\)
Để G là trọng tâm tam giác ABC thì: \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 3{x_G} - {x_A} - {x_B}\\{y_C} = 3{y_G} - {y_A} - {y_B}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 3.1 - \left( { - 1} \right) - 1 = 3\\{y_C} = 3.2 - 1 - 5 = 0\end{array} \right.\)
Vậy tọa độ điểm C là: \(C\left( {3;0} \right)\)
7 tháng 6 2015
2 Vì O nằm trên đường thẳng xy suy ra tia Ox đối với tia Oy(*)
mà A thuộc tia Ox
B thuộc tia Oy
mà từ (*) ta có tia OA đối với tia OB suy ra điểm O nằm giữa A,B(**)
từ(**) ta có OA+OB=AB(công thức cộng đoạn thẳng )
3cm+5cm=AB
suy ra AB=8cm
b,TH1 M nằm trên tia OA
vì tia OA là tia đối của tia OB
suy ra tia OM là tia đói của tia OB
suy ra điểm O nằm giữa diểm M,B
suy ra ta có
OM+OB=MB(công thức cộng đoạn thẳng)
1cm+5cm=MB
suy ra MB=6cm
TH2 điểm M nằm trên tia Oy
vì trên tia Oy có điểm M,B(1)
mà OM<OB vì (1cm<5cm)(2)
suy ra diểm M nằm giữa điểm O,B(***)
từ (***) suy ra OM+MB=OB(công thức cộng góc)
1cm+MB=5cm
MB=5cm-1cm
MB=4cm
còn câu a tớ ko biết
C thuộc(Δ)nên C(5-3a,a)
1) để ΔABC cân tại C thì AC=BC hay AC2=BC2
mà AC2=(6-3a)2+(a-3)2 BC2=(3-3a)2+(a-2)2
=======>(6-3a)2+(a-3)2=(3-3a)2+(a-2)2
<=> a=8/5======>C(1/5,8/5)
2)ΔABD vuông tại A thì
\(\overrightarrow{AB}\) x \(\overrightarrow{AD}\)=0 do D thuộcΔ nen D(5-3b,b)
\(\overrightarrow{AB}\)=(3,-1)
\(\overrightarrow{AD}\)=(6-3b,b-3)========>3x(6-3b)-1x(b-3)=0
<=>b=21/10=========>D(-13/10,21/10)