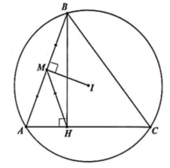
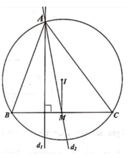
trong mặt phẳng tọa độ oxy cho tam giác ABC. Gọi D là chân đường phân giác kẻ từ A .tâm đường tròn ngoại tiếp tam giác ABC và ABD lần lượt là I(2;1) và E(5/3;2). Phương trình AD:x-y=0 và điểm A có hoành độ lớn hơn 2. tìm tọa độ điểm A,B,C
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 4 2016
Ta có \(HK\perp BC,K\in BC;\overrightarrow{HK}=\left(0;-2\right)\Rightarrow y-1=0\)
Gọi M là trung điểm của BC ta có phương trình \(x+3=0;M=IM\cap BC\Rightarrow M\left(-3;1\right)\)
Gọi D là điểm đối xứng của A qua I chỉ ra BHCD là hình bình hành. Khi đó M là trung điểm của HD, suy ra D(-5;-1).
I là trung điểm của AD, suy ra A(-1;7)
\(AI=\sqrt{20}\), phương trình đường tròn ngoại tiếp tam giác ABC là : \(\left(x+3\right)^2+\left(y-3\right)^2=20\)
Tọa độ điểm B, C là nghiệm của hệ phương trình :
\(\begin{cases}y-1=0\\\left(x+3\right)^2+\left(y-3\right)^2=20\end{cases}\)\(\Leftrightarrow\begin{cases}x=1\\y=1\end{cases}\) hoặc \(\begin{cases}x=-7\\y=1\end{cases}\)
Vậy ta có \(B\left(1;1\right),C\left(-7;1\right)\) hoặc \(B\left(-7;1\right),C\left(1;1\right)\)
Suy ra \(A\left(-1;7\right);B\left(1;1\right),C\left(-7;1\right)\)
hoặc\(A\left(-1;7\right);B\left(-7;1\right),C\left(1;1\right)\)
CX
28 tháng 11 2021
Tham khảo!
Gợi ý: Gọi H là trực tâm tam giác ABC. Dễ dàng chứng minh được AD là phân giác góc EDF.
=> BD là phân giác góc FDG.
=> FG đối xứng với nhau qua BC.
=> BG vuông góc GC
Vẽ đường GC tìm được tọa độ của C
Vẽ đường BC.
Gọi I là giao điểm của FG và BC tìm tọa độ của I có I rồi tìm được tọa độ của F có F thì vẽ được đường thẳng AB.
7 tháng 4 2016
Do \(\widehat{AIB}=90^0\Rightarrow\widehat{ACB}=45^0\) hoặc \(\widehat{ACB}=135^0\Rightarrow\widehat{ACD}=45^0\Rightarrow\Delta ACD\) vuông cân tại D nên DA=DC
Hơn nữa IA=IC => \(DI\perp AC\Rightarrow\) đường thẳng AC thỏa mãn điều kiện AC qua điểm M và AC vuông góc ID.
Viết phương trình đường thẳng AC : \(x-2y+9=0\)
Gọi \(A\left(2a-9;a\right)\in AC\). Do \(DA=\sqrt{2}d\left(D,AC\right)=2\sqrt{10}\) nên
\(\sqrt{\left(2a-8\right)^2+\left(a+1\right)^2}=2\sqrt{10}\Leftrightarrow a^2-6a+5=0\)
\(\Leftrightarrow\begin{cases}a=1\Rightarrow A\left(-7;1\right)\\a=5\Rightarrow A\left(1;5\right)\end{cases}\)
Theo giả thiết đầu bài \(\Rightarrow A\left(1;5\right)\)
Viết phương trình đường thẳng DB : \(x+3y+4=0\). Gọi \(B\left(-3b-4;b\right)\)
Tam giác IAB vuông tại I nên : \(\overrightarrow{IA.}\overrightarrow{IB}=0\Leftrightarrow3\left(-3b-2\right)+4\left(b-1\right)=0\Leftrightarrow b=-2\Rightarrow B\left(2;-2\right)\)
Đáp số \(A\left(1;5\right);B\left(2;-2\right)\)