Có bao nhiêu giá trị nguyên m ∈ (-10; 10) để hàm số y = m2x4 - 2(4m - 1)x2 + 1 đồng biến trên khoảng (1; +\(\infty\) )
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
9 tháng 9 2017
Nếu m = 0 thì phương trình trở thành 1 = 0 : vô nghiệm.
Khi m ≠ 0 , phương trình đã cho có nghiệm khi và chỉ khi
∆ = m 2 - 4 m ≥ 0 ⇔ m ≤ 0 m ≥ 4
Kết hợp điều kiện m ≠ 0 , ta được m < 0 m ≥ 4
Mà m ∈ Z và m ∈ [−10; 10] ⇒ m ∈ {−10; −9; −8;...; −1} ∪ {4; 5; 6;...; 10}.
Vậy có tất cả 17 giá trị nguyên m thỏa mãn bài toán.
Đáp án cần chọn là: A
CM
5 tháng 8 2017
Đáp án C
Đặt m + e x = a ; e x = b a ≥ 0 ; b > 0 ta có:
m + b = a m + a = b ⇔ m + b = a 2 m + a = b 2
⇔ m + b = a 2 b − a = a 2 − b 2 ⇔ m + b = a 2 a − b a + b + 1 = 0 ⇒ m = a 2 − b a = b
( Do a ≥ 0 ; b > 0 )
Khi đó m = b 2 − b b > 0
Do b 2 − b ≥ − 1 4 ∀ b > 0 nên phương trình có nghiệm khi m ≥ − 1 4
Do đó có 10 giá trị nguyên của m ∈ − 1 4 ; 10 thỏa mãn yêu cầu bài toán.
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 2 2021
\(g\left(x\right)=3x^4-4x^3-6mx^2+12mx\)
\(g'\left(x\right)=12x^3-12x^2-12mx+12m=0\)
\(\Leftrightarrow12x^2\left(x-1\right)-12m\left(x-1\right)=0\)
\(\Leftrightarrow12\left(x^2-m\right)\left(x-1\right)=0\Rightarrow\left[{}\begin{matrix}x=1\\x^2=m\end{matrix}\right.\)
Xét \(g\left(x\right)=0\Leftrightarrow x\left(3x^3-4x^2-6mx+12m\right)=0\)
- Nếu \(m=0\Rightarrow g'\left(x\right)=0\) có 1 nghiệm bội lẻ, \(g\left(x\right)=0\) có 2 nghiệm bội lẻ \(\Rightarrow f\left(x\right)\) có 3 cực trị (thỏa mãn)
- Nếu \(m=\dfrac{1}{6}\Rightarrow g'\left(x\right)=0\) có 3 nghiệm bội lẻ, \(g\left(x\right)=0\) có 3 nghiệm pb nhưng chỉ có 1 nghiệm \(x=1\) trùng với \(g'\left(x\right)=0\) nên hàm có 5 cực trị (ktm)
- Nếu \(m=1\Rightarrow g'\left(x\right)=0\) có 1 nghiệm bội lẻ, \(g\left(x\right)=0\) có 2 nghiệm bội lẻ (thỏa mãn)
- Nếu \(m< 0\Rightarrow g'\left(x\right)=0\) có 1 nghiệm bội lẻ \(x=1\)
Khi đó hàm có 3 cực trị khi \(g\left(x\right)=0\) có 2 nghiệm bội lẻ (hiển nhiên từ các TH này thì \(g\left(x\right)=0\) ko thể có nghiệm \(x=1\) do đã loại trừ từ TH \(m=\dfrac{1}{6}\))
\(\Leftrightarrow3x^3-4x^2-6mx+12m=0\) có đúng 1 nghiệm
\(\Leftrightarrow3x^3-4x^2=6m\left(x-2\right)\Leftrightarrow m=\dfrac{3x^3-4x^2}{6\left(x-2\right)}\) (do \(x=2\) ko là nghiệm)
Khảo sat \(h\left(x\right)=\dfrac{3x^3-4x^2}{6\left(x-2\right)}\) ta được \(y=m\) cắt \(y=h\left(x\right)\) tại đúng 1 điểm khi: \(\left[{}\begin{matrix}m< 0\\\dfrac{1}{6}< m< \dfrac{64}{9}\\\end{matrix}\right.\) \(\Leftrightarrow m< 0\)
- Nếu \(m>0;m\ne\left\{\dfrac{1}{6};1\right\}\) \(\Rightarrow g'\left(x\right)=0\) có 3 nghiệm pb
Mà \(g\left(x\right)=0\) luôn có ít nhất 1 nghiệm bội lẻ \(x=0\)
\(\Rightarrow\) Hàm có 3 cực trị khi và chỉ khi:
TH1: \(3x^3-4x^2-6mx+12m=0\) vô nghiệm (vô lý do hàm bậc 3 luôn có nghiệm)
Th2: \(3x^3-4x^2-6mx+12m=0\) (1) có 3 nghiệm đều trùng với nghiệm của \(g'\left(x\right)=0\) (vô lý do \(m\ne\dfrac{1}{6}\) nên nếu (1) có nghiệm thì nó luôn có nghiệm khác 1)
Kết luận: \(\left[{}\begin{matrix}m=1\\m\le0\end{matrix}\right.\)
MN
26 tháng 2 2021
lúc đầu mk giải câu này theo kiểu xét 3 trường hợp là m < 0; 1 nằm giữa hai nghiệm kia; 1 nằm bên phải 2 nghiệm kia. Không biêt cách này có đúng không mà tính ra kết quả là 10 giá trị ???
17 tháng 12 2023
Để tìm số giá trị nguyên của m trong khoảng [-10;10] sao cho giá trị lớn nhất của hàm số y = -x^4 + 4x - m trên đoạn [-1;3] nhỏ hơn 10, chúng ta cần thực hiện các bước sau:
1. Tìm giá trị lớn nhất của hàm số y = -x^4 + 4x - m trên đoạn [-1;3].
2. Kiểm tra xem giá trị lớn nhất của hàm số có nhỏ hơn 10 hay không.
3. Đếm số giá trị nguyên của m trong khoảng [-10;10] thỏa mãn điều kiện trên.
Bước 1: Tìm giá trị lớn nhất của hàm số y = -x^4 + 4x - m trên đoạn [-1;3].
Để tìm giá trị lớn nhất, chúng ta có thể lấy đạo hàm của hàm số và giải phương trình đạo hàm bằng 0.
y' = -4x^3 + 4
Để tìm giá trị của x khi đạo hàm bằng 0, giải phương trình:
-4x^3 + 4 = 0
X^3 - 1 = 0
( x - 1)( x^2 + x + 1) = 0
Phương trình có 2 nghiệm: x = 1 và x^2 + x + 1 =0 (phương trình bậc 2).
Bước 2: Kiểm tra giá trị lớn nhất của hàm số có nhỏ hơn 10 hay không.
Để kiểm tra giá trị lớn nhất của hàm số, chúng ta có thể thay x = 1 vào hàm số:
y = - 1^4(1) - m = 3 - m
Điều kiện y < 10:
3 - m < 10
- m < 7
m > -7
Bước 3: Đếm số giá trị nguyên của m trong khoảng [-10;10] thỏa mãn điều kiện trên.
Trong khoảng [-10;10], có 17 giá trị nguyên. Tuy nhiên, chúng ta chỉ quan tâm đến các giá trị m > -7.
Vậy, có 17 - 7 = 10 giá trị nguyên của m trong khoảng [-10;10] thỏa mãn điều kiện y < 10.
CM
27 tháng 4 2018
Vậy có 8 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Đáp án D
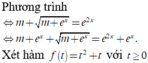
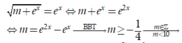
- Với \(m=0\) thỏa mãn
- Với \(-2\left(4m-1\right)\ge0\Rightarrow m\le\dfrac{1}{4}\) hàm đồng biến trên \(\left(0;+\infty\right)\) thỏa mãn
- Xét với \(m>\dfrac{1}{4}\)
\(y'=4m^2x^3-4x\left(4m-1\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{\sqrt{4m-1}}{m}\\x=-\dfrac{\sqrt{4m-1}}{m}\end{matrix}\right.\)
Do \(a=m^2>0\) nên hàm đồng biến trên các khoảng \(\left(-\dfrac{\sqrt{4m-1}}{m};0\right)\) và \(\left(\dfrac{\sqrt{4m-1}}{m};+\infty\right)\)
\(\Rightarrow\) Hàm đồng biến trên khoảng đã cho khi và chỉ khi:
\(\dfrac{\sqrt{4m-1}}{m}\ge1\Rightarrow4m-1\ge m^2\)
\(\Leftrightarrow m^2-4m+1\le0\Rightarrow2-\sqrt{3}\le m\le2+\sqrt{3}\)
Vậy \(\left[{}\begin{matrix}m\le\dfrac{1}{4}\\2-\sqrt{3}\le m\le2+\sqrt{3}\end{matrix}\right.\)