Cho hàm số FX có đạo hàm liên tục trên đoạn [0;1] bằng mãn f (1) = 1 và (f'(x))²+4(6x²-1).f(x)=40x⁶-44x⁴+32x²-4,Tích phân cân từ 0 đến 1 của xf(x)dx bằng
A.-13/15
B.5/12
C.13/15
B.-5/12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có
![]()
![]()
![]()
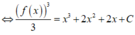
![]()
Ta có: f ( 0 ) = 1 ⇒ 1 = 3 C
![]()
![]()
Xét hàm ![]() trên [-2;1]
trên [-2;1]
Ta có
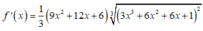
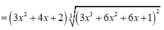
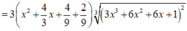
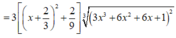
Nhận thấy f ' ( x ) > 0 ∀ x ∈ ℝ ⇒ Hàm số đồng biến trên (-2;1)
Suy ra m a x - 2 ; 1 f ( x ) = f ( 1 ) = 16 3
Chọn đáp án C.
Lấy tích phân 2 vế:
\(\int\limits^1_0\left[f'\left(x\right)\right]^2dx+\int\limits^1_04\left(6x^2-1\right)f\left(x\right)dx=\int\limits^1_0\left(40x^6-44x^4+32x^2-4\right)dx=\frac{376}{105}\)
Xét \(I=\int\limits^1_0\left(6x^2-1\right)f\left(x\right)dx\)
Đặt \(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=\left(6x^2-1\right)dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=2x^3-x\end{matrix}\right.\)
\(\Rightarrow I=\left(2x^3-x\right)f\left(x\right)|^1_0-\int\limits^1_0\left(2x^3-x\right)f'\left(x\right)dx=1-\int\limits^1_0\left(2x^3-x\right)f'\left(x\right)dx\)
\(\Rightarrow\int\limits^1_0\left[f'\left(x\right)\right]^2dx+4-4\int\limits^1_0\left(2x^3-x\right)f'\left(x\right)dx=\frac{376}{105}\)
\(\Leftrightarrow\int\limits^1_0\left[f'\left(x\right)-2\left(2x^3-x\right)\right]^2dx-\int\limits^1_04\left(2x^3-x\right)^2dx=-\frac{44}{105}\)
\(\Leftrightarrow\int\limits^1_0\left[f'\left(x\right)-2\left(2x^3-x\right)\right]^2dx-\frac{44}{105}=-\frac{44}{105}\)
\(\Leftrightarrow\int\limits^1_0\left[f'\left(x\right)-\left(4x^3-2x\right)\right]^2dx=0\)
\(\Rightarrow f'\left(x\right)=4x^3-2x\Rightarrow f\left(x\right)=x^4-x^2+C\)
\(f\left(1\right)=1\Rightarrow1-1+C=1\Rightarrow C=1\)
\(\Rightarrow f\left(x\right)=x^4-x^2+1\)
\(\Rightarrow\int\limits^1_0x\left(x^4-x^2+1\right)dx=\frac{5}{12}\)