Cho hình chữ nhật (H) có đỉnh A(-2;1) và phương trình hai cạnh của hình chữ nhật là x – 2y + 1 = 0 và 2x + y – 4 = 0. Diện tích hình chữ nhật (H) là
A. 19/5
B. 21/5
C. 23/5
D. 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D
Phương pháp
Nhận xét rằng: Đa giác đều có số đỉnh chẵn luôn tồn tại đường kính của đường tròn ngoại tiếp đa giác là đoạn nối hai đỉnh của đa giác.
Nên ta chia đường tròn ngoại tiếp đa giác đều đó thành hai nửa đường tròn và dựa vào tính đối xứng của các đỉnh để tạo thành một hình chữ nhật.
Tính số hình vuông trong các hình chữ nhật đó để tính xác suất 4 đỉnh tạo thành hình chữ nhật mà không phải hình vuông.
Cách giải
Số phần tử của không gian mẫu n Ω = C 24 4
Ta vẽ đường tròn ngoại tiếp đa giác đều 24 đỉnh. Vẽ một đường kính của đường tròn này. Khi đó hai nửa đường tròn đều chứa 12 đỉnh.
Với mỗi đỉnh thuộc nửa đường tròn thứ nhất ta đều có một đỉnh đối xứng với nó qua đường kính và thuộc nửa đường tròn còn lại.
Như vậy cứ hai đỉnh thuộc nửa đường tròn thứ nhất ta xác định được hai đỉnh đối xứng với nó qua đường kính và thuộc nửa đường tròn còn lại, bốn đỉnh này tạo thành một hình chữ nhật.
Vậy số hình chữ nhật có 4 đỉnh là các đỉnh của đa giác đã cho là C 12 2 .
Nhận thấy rằng trong số các hình chữ nhật tạo thành có 24:4=6 hình vuông (vì hình chữ nhật có các cạnh bằng nhau là hình vuông)
Nên số hình chữ nhật mà không phải hình vuông là C 12 2 - 6 .
Xác suất cần tìm là
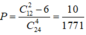

Vì ∆ ABC đồng dạng với ∆ AMN nên:
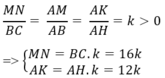
Diện tích hình chữ nhật MNPQ là:
SMNPQ = MN. NP = MN.KH = MN.( AH – AK)
=> SMNPQ = 16k.( 12- 12k)
Theo đề bài diện tích hình chữ nhật đó là 36cm2 nên
16k.( 12- 12k ) = 36
⇔ 16k.12( 1- k) = 36
⇔ 16k(1 – k) = 3 ( chia cả hai vế cho 12)
⇔ 16k – 16k2 = 3
⇔ 16k2- 16k + 3= 0
Ta có: ∆’= (-8)2 – 16.3 = 16> 0
Phương trình trên có 2 nghiệm là:
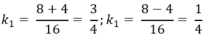
Vậy để diện tích hình chữ nhật MNPQ là 36cm2 thì vị trí điểm M phải thỏa mãn:
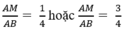

Vì ∆ ABC đồng dạng với ∆ AMN nên:
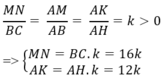
Diện tích hình chữ nhật MNPQ là:
SMNPQ = MN. NP = MN.KH = MN.( AH – AK)
=> SMNPQ = 16k.( 12- 12k)
Theo đề bài diện tích hình chữ nhật đó là 36cm2 nên
16k.( 12- 12k ) = 36
⇔ 16k.12( 1- k) = 36
⇔ 16k(1 – k) = 3 ( chia cả hai vế cho 12)
⇔ 16k – 16k2 = 3
⇔ 16k2- 16k + 3= 0
Ta có: ∆’= (-8)2 – 16.3 = 16> 0
Phương trình trên có 2 nghiệm là:
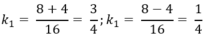
Vậy để diện tích hình chữ nhật MNPQ là 36cm2 thì vị trí điểm M phải thỏa mãn:
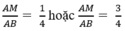

a) Đặt tên các điểm như hình vẽ.
Giả sử BC = a; BM = x. Ta có MN = QP = a - 2x
Áp dụng định lý Ta let ta có:
\(\frac{AQ}{AB}=\frac{QP}{BC}\Rightarrow AQ=\frac{AB.QP}{BC}=a-2x\)
\(\Rightarrow QB=AB-AQ=a-\left(a-2x\right)=2x\)
\(\Rightarrow QM=\sqrt{QB^2-BM^2}=\sqrt{4x^2-x^2}=x\sqrt{3}\)
\(\Rightarrow S_{MNPQ}=MN.QM=\left(a-2x\right).x\sqrt{3}\)
\(=-2\sqrt{3}x^2+a\sqrt{3}x\)
\(=-2\sqrt{3}\left(x^2-2.\frac{a}{4}.x+\frac{a^2}{16}\right)+\frac{a^2\sqrt{3}}{8}\)
\(=-2\sqrt{3}\left(x-\frac{a}{4}\right)^2+\frac{a^2\sqrt{3}}{8}\le\frac{a^2\sqrt{3}}{8}\)
Vậy diện tích lớn nhất của hình chữ nhật là \(\frac{a^2\sqrt{3}}{8}\) khi BM = BC/4
b) Em tham khảo tại đây nhé.
Câu hỏi của Nguyễn Tuấn Minh - Toán lớp 8 - Học toán với OnlineMath

Tham khảo
Diện tích hình chữ nhật ABCD là:
`12 × 5 = 60 (cm2)`
Điểm N là trung điểm của đoạn thẳng DC nên độ dài đoạn thẳng NC là:
12:2=6(cm)12:2=6(cm)
Diện tích hình bình hành AMCN là:
5×6=30(cm²)5×6=30(cm2)
Vậy diện tích hình chữ nhật ABCD gấp hai lần diện tích hình bình hành AMCN.

Tham Khảo
Hình chữ nhật ABCD có chiều dài 12cm, chiều rộng 5cm.
Áp dụng công thức : Shcn = chiều dài x chiều rộng
Diện tích hình chữ nhật ABCD là:
12 x 5 = 60 (cm2)

tham Khảo:
DC là chiều dài của hình chữ nhật nên DC = 12cm. Mà N là trung điểm của cạnh DC nên độ dài đoạn thẳng NC là:
12 : 2 = 6 (cm)
Hình bình hành AMCN có chiều cao MN = 5cm và đáy NC = 6cm.
Áp dụng công thức : Shbh = MN x NC
Diện tích hình bình hành AMCN bằng:
6 x 5 = 30 (cm2)
Ta thấy điểm A không thuộc 2 đường thẳng đã cho.
Khoảng cách từ A đến 2 đường thẳng là:
Đáp án B