Trên hệ tọa độ Oxy,cho A(-1;3);B(2;4);C(0;1) .Tìm điểm E thuộc đường thẳng d:y=x+1 sao cho ABEC là hình thang
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi \(M\left(0;m\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(-1;m+2\right)\\\overrightarrow{AB}=\left(-5;7\right)\end{matrix}\right.\)
3 điểm M;A;B thẳng hàng khi:
\(\dfrac{-1}{-5}=\dfrac{m+2}{7}\Rightarrow m=-\dfrac{3}{5}\)
\(\Rightarrow M\left(0;-\dfrac{3}{5}\right)\)

Biểu diễn ba điểm A, B, C trên hệ trục tọa độ Oxy ta được
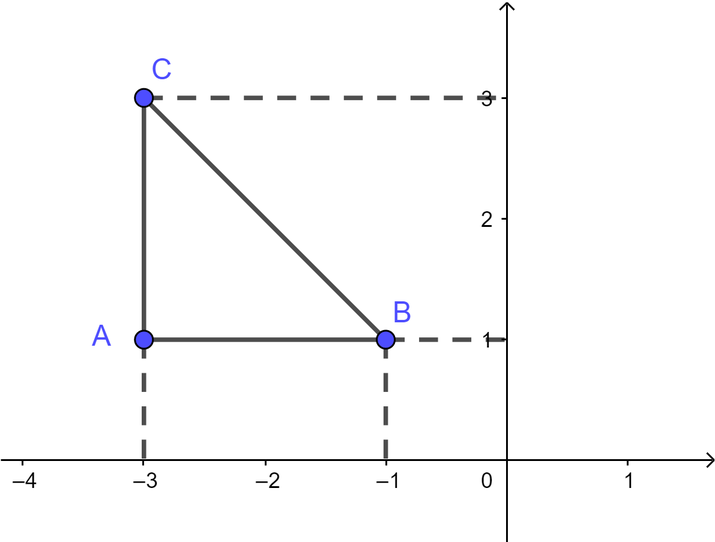
Quan sát hình vẽ ta thấy tam giác ABC là tam giác vuông tại A
Chọn đáp án C

\(\overrightarrow{AB}=\left(-1;1\right)\) nên pt AB có dạng:
\(1\left(x-2\right)+1\left(y-3\right)=0\Leftrightarrow x+y-5=0\)
Do I thuộc AB nên tọa độ có dạng: \(I\left(a;5-a\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{IA}=\left(2-a;a-2\right)\\\overrightarrow{IB}=\left(1-a;a-1\right)\\\overrightarrow{IC}=\left(-1-a;a-10\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{IA}+3\overrightarrow{IB}+5\overrightarrow{IC}=\left(-9a;9a-55\right)\)
\(\Rightarrow\left|\overrightarrow{IA}+3\overrightarrow{IB}+5\overrightarrow{IC}\right|=\sqrt{\left(9a\right)^2+\left(55-9a\right)^2}\ge\sqrt{\dfrac{1}{2}\left(9a+55-9a\right)^2}=\dfrac{55}{\sqrt{2}}\)
Dấu "=" xảy ra khi \(9a=55-9a\Rightarrow a=\dfrac{55}{18}\Rightarrow I\left(\dfrac{55}{18};\dfrac{35}{18}\right)\)
Kiểm tra lại tính toán

Đường thẳng đi qua hai điểm A và B có dạng: y = ax + b
Đường thẳng đi qua hai điểm A và B nên tọa độ A và B nghiệm đúng phương trình.
Ta có: Tại A: 2 = a + b ⇔ b = 2 – a (1)
Tại B: 4 = 3a + b (2)
Thay (1) và (2) ta có: 4 = 3a + 2 – a ⇔ 2a = 2 ⇔ a = 1
Vậy hệ số a của đường thẳng đi qua A và B là 1.

\(\overrightarrow{AB}=\left(x_B-x_A;y_B-y_A\right)=\left(3;-9\right)\)
\(\overrightarrow{AC}=\left(1;-2\right)\) ; \(\overrightarrow{BC}=\left(-2;-3\right)\)
\(C\in d\) ; \(\overrightarrow{u_d}=\left(1;1\right)\) ; \(\overrightarrow{AB}=\left(3;1\right)\Rightarrow AB\) không song song với d
\(\Rightarrow ABEC\) là hình thang khi và chỉ khi AC//BE hoặc BC//AE
Gọi \(E\left(x;x+1\right)\Rightarrow\overrightarrow{BE}=\left(x-2;x-3\right)\) ; \(\overrightarrow{AE}=\left(x+1;x-3\right)\)
\(\Rightarrow\left[{}\begin{matrix}\frac{x-2}{1}=\frac{x-3}{-2}\\\frac{x+1}{-2}=\frac{x-3}{-3}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\frac{7}{3}\\x=-9\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}E\left(\frac{7}{3};\frac{10}{3}\right)\\E\left(-9;-8\right)\end{matrix}\right.\)