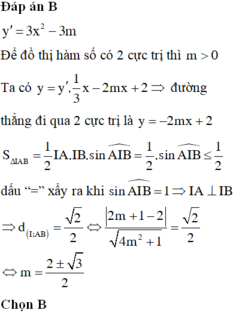tìm m để đt đi qua cđ, ct của hs y=x3-3mx+2 cắt đường tròn tâm I(1;1), bán kính =1 tại 2 điểm pb A,B sao cho SIAB max
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn B
[Phương pháp tự luận]
y ' = 3 x 2 - 3 m
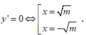
Hàm số có 2 cực trị khi và chỉ khi m > 0
Khi đó tọa độ 2 điểm cực trị của đồ thị hàm số là : M ( m ; - 2 m m + 2 )
![]()
Phương trình đt MN : 2 m x + y - 2 = 0
![]()
![]()
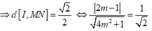
⇔ m = 1 ± 3 2

Đạo hàm y’ = 3x2 – 3m
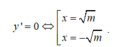
Hàm số có 2 cực trị khi và chỉ khi : m> 0
Khi đó tọa độ 2 điểm cực trị của đồ thị hàm số là:
M ( m ; - 2 m m + 2 ) N ( - m ; 2 m m + 2 ) ⇒ M N → = ( - 2 m ; 4 m m )
Phương trình đường thẳng MN: 2mx+ y-2=0
Ta có :
S ∆ I A B = 1 2 I A . I B . sin A I B ^ = 1 2 sin A I B ^ ≤ 1 2
Dấu bằng xảy ra khi
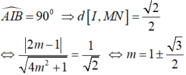
Chọn B.

Chọn C
![]() .
.
Vì ![]() nên phương trình
nên phương trình ![]() có 2 nghiệm phân biệt.
có 2 nghiệm phân biệt.
Do đó hàm số có hai điểm cực trị ![]() .
.
Giả sử hàm số có hai điểm cực trị lần lượt là ![]() và
và ![]() , với
, với ![]() ,
, ![]() là nghiệm của phương trình
là nghiệm của phương trình ![]() .
.
Thực hiện phép chia ![]() cho
cho ![]() ta được :
ta được : ![]() .
.
Khi đó ta có: 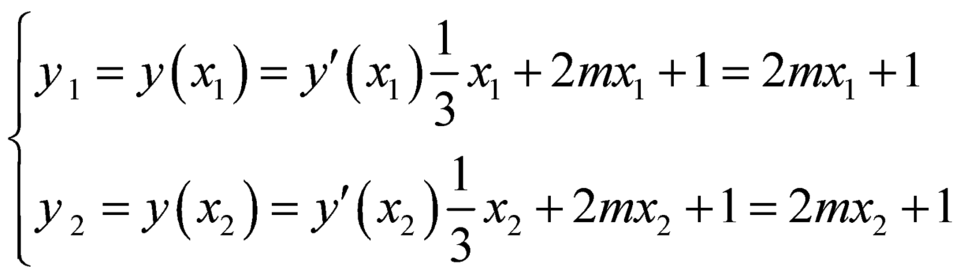 .
.
Ta thấy, toạ độ hai điểm ![]() và
và ![]() thoả mãn phương trình
thoả mãn phương trình ![]() .
.
Do đó, phương trình đường thẳng qua hai điểm cực trị là ![]() .
.
Ta thấy ![]() luôn qua
luôn qua ![]() .
.
Đặt ![]()
![]() .
.
![]() .
.
Xét hàm số ![]() ,
, ![]() .
.
![]() ,
, ![]() .
.
Suy ra hàm số ![]() liên tục và đồng biến trên
liên tục và đồng biến trên ![]() .
.
Do đó ![]() .
.
Vậy ![]() đạt giá trị lớn nhất
đạt giá trị lớn nhất ![]()
![]() .
.

\(y'=3x^2-6x-m\)
Hàm số có CĐ, CT khi \(y'=0\) có 2 nghiệm pb
\(\Rightarrow\Delta'=9+3m>0\Rightarrow m>-3\)
Tiến hành chia y cho y' và lấy phần dư ta được phương trình đường thẳng qua CĐ, CT có dạng:
\(y=-\left(\dfrac{2m}{3}+2\right)x-\dfrac{m}{3}+2\)
Do đường thẳng tạo với 2 trục 1 tam giác vuông cân nên có hệ số góc bằng 1 hoặc -1
\(\Rightarrow\left[{}\begin{matrix}-\left(\dfrac{2m}{3}+2\right)=1\\-\left(\dfrac{2m}{3}+2\right)=-1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=-\dfrac{9}{2}< -3\left(loại\right)\\m=-\dfrac{3}{2}\end{matrix}\right.\)