Tìm m,n biết rằng đường thẳng d1: y=2mx+4n đi qua điểm A(2;0) và song song với đường thẳng d2:y=4x+3.
Mấy bn giải giúp mik vs, mik đang cần gấp.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) Vì (d) song song với (d2) nên 2m=4
hay m=2
hay (d): y=4x+4n
Vì (d) đi qua A(2;0) nên Thay x=2 và y=0 vào (d), ta được:
\(4\cdot2+4\cdot n=0\)
\(\Leftrightarrow4\cdot n=-8\)
hay n=-2
Vậy: m=2; n=-2
- Ta có : đường thẳng d song song với đường thẳng d2 .
\(\Rightarrow\left\{{}\begin{matrix}a=a^,\\b\ne b^,\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2m=4\\4n\ne3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m=2\\n\ne\dfrac{3}{4}\end{matrix}\right.\)
- Thay m vào đường thẳng ta được : \(y=4x+4n\)
Lại có : d đi qua điểm A .
- Thay tọa độ của A vào đường thẳng ta được :
\(0=4.2+4n\)
\(\Leftrightarrow n=-2\left(TM\right)\)
Vậy ...

(d1) đi qua A => thay x=2, y=0 vào hàm số ta có: 0=4m+4n=> 4(m+n)=0 <=> m+n=0
d1//d2=> a=a' và b khác b' hay 2m=4 và 4n khác 3 <=> m=2 => n=-2(t/m đk)
=> m=2 và n=-2

Vì (d1)//(d2) nên 4m=4 ⇔ m=1
Khi đó ta có pt (d1): y=4x+n
Vì (d2) đi qua điểm A(2;0) nên ta có:
0=4\(\times\)2+n ⇔ 8+n=0 ⇔ n=\(_{^{ }-8}\)
Vậy m=1 và n= -8

Vì (d1) đi qua điểm A(2;0) nên \(\Rightarrow\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\)
Hay \(4m+4n=0\Leftrightarrow m+n=0\) (1)
Vì (d1) song song với (d2): y = 4x + 3 nên: \(\left\{{}\begin{matrix}2m=4\\4n\ne3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=2\\n\ne\frac{3}{4}\end{matrix}\right.\) (2)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}m=2\\n=-2\end{matrix}\right.\) ( thỏa mãn )
Vậy...

*Đường thẳng ( d 1 ): ax + 2y = -3 đi qua điểm M(3; 9) nên tọa độ điểm M nghiệm đúng phương trình đường thẳng.
Ta có: a.3 + 2.9 = -3 ⇔ 3a + 18 = -3 ⇔ 3a = -21 ⇔ a = -7
Phương trình đường thẳng ( d 1 ): -7x + 2y = -3
*Đường thẳng ( d 2 ): 3x – by = 5 đi qua điểm N(-1; 2) nên tọa độ điểm N nghiệm đúng phương trình đường thẳng.
Ta có: 3.(-1) – b.2 = 5 ⇔ -3 – 2b = 5 ⇔ 2b = -8 ⇔ b = -4
Phương trình đường thẳng ( d 2 ): 3x + 4y = 5
*Tọa độ giao điểm của (
d
1
) và (
d
2
) là nghiệm của hệ phương trình: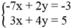
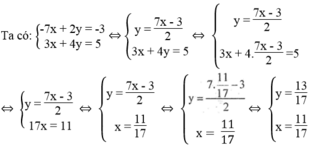
(d1) đi qua A => thay x = 2 , y = 0 vào hàm số ta có : 0 = 4m + 4n => 4(m+n) = 0 <=> m - n = 0
d1//d2 => a=a' và b khác b' hay 2m = 4 và 4n khác 3 <=> m = 2 => n = -2(t/m đk)
=> m = 2 và n = -2