Phương trình đường thẳng đi qua hai điểm M(-2;1) và N(2;0) là:
A. y = 2 x + 1
B. y= -2x + 4
C. y = - 1 4 x + 1 2
D. y = 3x + 7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 4 2023
a: vecto AB=(-1;6)
=>VTPT là (6;1)
Phương trình tham số là;
x=1-t và y=-2+6t
b: PTTQ là:
6(x-1)+1(y+2)=0
=>6x-6+y+2=0
=>6x+y-4=0
MN
3 tháng 6 2021
c)
(d) vuông góc với (d') : y = 2x
=> (d) có dạng : y = -2x + b
(d) đi qua M (3,5) :
5 = (-2) . 3 + b
=> b = 10
(d) : y = -2x + 10
DD
0
PP
2
14 tháng 4 2022
Vì (d): y=ax+b đi qua M(-2/3;-7) và N(2;1) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}-\dfrac{2}{3}a+b=-7\\2a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=-5\end{matrix}\right.\)
HN
14 tháng 4 2022
\(\overrightarrow{MN}\)=(8/3;8)=8/3.(1;3).
Phương trình đường thẳng cần tìm đi qua N(2;1) và nhận vectơ \(\overrightarrow{n}\)=(3;-1) làm một vectơ pháp tuyến.
MN: 3(x-2)-1(y-1)=0 \(\Leftrightarrow\) 3x-y-5=0.
CM
28 tháng 3 2017
Chọn B
Gọi đường thẳng cần tìm là Δ, A là giao của Δ và d.
Khi đó: A (2+3t;-3+2t;1+t), 
Do Δ vuông góc với d' nên:
Khi đó 
, hay vectơ chỉ phương của Δ là (3;-1;0).
Vậy phương trình Δ: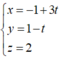 
AT
31 tháng 5 2021
a) Gọi pt đường thẳng (d) là : \(y=ax+b\left(a\ne0\right)\)
Vì (d) có hệ số góc là 2 \(\Rightarrow a=2\Rightarrow y=2x+b\)
Vì đường thẳng d đi qua điểm \(M\left(-1;3\right)\)
\(\Rightarrow3=-2+b\Rightarrow b=5\Rightarrow y=2x+5\)
b) Gọi pt đường thẳng d là \(y=ax+b\left(a\ne0\right)\)
Vì \((d)\parallel (d')\Rightarrow a=2\Rightarrow y=2x+b\)
Vì đường thẳng d đi qua điểm \(M\left(3;5\right)\)
\(\Rightarrow5=6+b\Rightarrow b=-1\Rightarrow y=2x-1\)
Đáp án là C