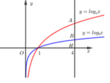
Cho điểm H(4;0) đường thẳng x = 4 cắt hai đồ thị hàm số y = log a x và y = log b x lần lượt tại 2 điểm A, B sao cho A B = 2 B H . Khẳng định nào sau đây là đúng?
A. b = a 3
B. a = b 3
C. a = 3 b
D. b = 3 a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

M, N, P thẳng hàng nên chúng cùng nằm trên đường thẳng NP (1)
N, P, Q thẳng hàng nên chúng cùng nằm trên đường thẳng NP (2)
Từ (1) và (2) suy ra M, N, P, Q cùng nằm trên một đường thẳng (MN).

Bài 2 trước đã!
+) Ta có AB vuông góc với BD và AB = BD (gt)
=> ▲ ABD vuông cân tại B
=> ^BAD = 45° nên AD là phan giác ^BAC (*)
+) Từ trung điểm M của CE ta kẻ MH và MK lần lượt vuông góc với AB và AC
Ta có ^HBE = ^BCA (Cùng phụ ^ABC)
Mà ^EBM = ^BCM ( = 45°)
=> ^HBM = ^KCM
Lại có MB = MC (= ½ EC)
=>▲MHB = ▲MKC (c.h-g.n)
=> MH = MK hay M thuộc tia phân giác ^BAC (**)
Từ (*) và (**) ta có hai tia ADvà AM trùng nhau hay A, D, M thẳng hàng.

Ta có: \(\overrightarrow {AD} \left( { - 2;10} \right),{\mkern 1mu} \overrightarrow {AB} \left( { - 1;5} \right) \Rightarrow \overrightarrow {AD} = 2\overrightarrow {AB} \)
\(\Rightarrow\) 3 điểm \(A,B,D\) thẳng hàng.

- Tập xác định: D = R\ {1}
- Đạo hàm: 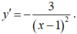
- Tung độ của tiếp tuyến là y = 4 nên :
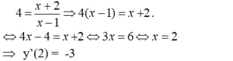
- Phương trình tiếp tuyến tại điểm M(2; 4) là:
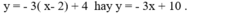
Chọn D.

a/ Gọi \(D\left(a;0\right)\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-9;3\right)\\\overrightarrow{AD}=\left(a-6;-3\right)\end{matrix}\right.\)
Do A; B; D thẳng hàng \(\Leftrightarrow\frac{a-6}{-9}=\frac{-3}{3}\Rightarrow a=15\) \(\Rightarrow D\left(15;0\right)\)
b/ \(\overrightarrow{AB}=\left(-1;5\right);\) \(\overrightarrow{AD}=\left(-2;10\right)\)
\(\Rightarrow\overrightarrow{AD}=2\overrightarrow{AB}\Rightarrow A,B,D\) thẳng hàng
Đáp án A
Ta có: A B = 2 B H ⇒ A H = 3 B H ⇒ log a 4 = 3 log b 4 ⇔ 1 log 4 a = 3 log 4 b ⇔ a 3 = b .