1. Trong mặt phẳng Oxy, có trọng tâm G(1,-1), M(2,1) và N(4,-2) lần lượt là trung điểm của AB, BC. Tìm tọa độ điểm B
2. Trong mặt phẳng Oxy, cho A(1,3), B(-2,2). Biết đường thẳng AB cắt trục tung tại điểm M(0,b). Giá trị b thuộc khoảng nào
3. Trong mặt phẳng tọa độ Oxy, cho A thỏa vecto OA= 2vecto i + 3vecto j. Tọa độ điểm A là
4. Trong mặt phẳng Oxy, cho vecto x=(1,2), vecto y=(3,4), vecto z=(5,-1). Tọa...
Đọc tiếp
1. Trong mặt phẳng Oxy, có trọng tâm G(1,-1), M(2,1) và N(4,-2) lần lượt là trung điểm của AB, BC. Tìm tọa độ điểm B
2. Trong mặt phẳng Oxy, cho A(1,3), B(-2,2). Biết đường thẳng AB cắt trục tung tại điểm M(0,b). Giá trị b thuộc khoảng nào
3. Trong mặt phẳng tọa độ Oxy, cho A thỏa vecto OA= 2vecto i + 3vecto j. Tọa độ điểm A là
4. Trong mặt phẳng Oxy, cho vecto x=(1,2), vecto y=(3,4), vecto z=(5,-1). Tọa độ vecto u = 2vecto x + vecto y - vecto z là
5. Trong mặt phẳng tọa độ Oxy, cho M(2,-3), N(4,7). Tọa độ trung điểm I của đoạn thẳng MN là
6. Cho vecto x=(-4,7) và hai vecto a=(2,-1), b=(-3,4). Nếu vecto x = m vecto a + n vecto b thì m, n là cặp số nào

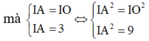
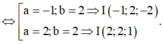
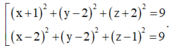

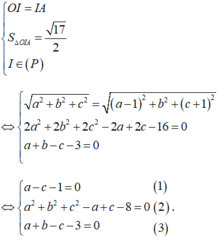
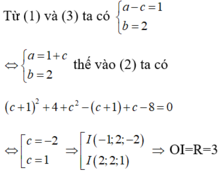

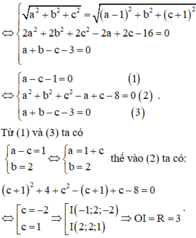
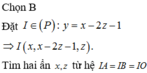
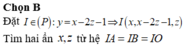

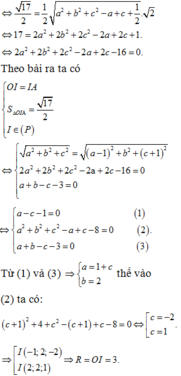
Gọi G là trọng tâm tam giác ABC. Ta có:
\(\left\{{}\begin{matrix}x_G=\dfrac{x_A+x_B+x_C}{3}=2\\y_G=\dfrac{y_A+y_B+y_C}{3}=3\end{matrix}\right.\) \(\Rightarrow G\left(2;3\right)\)
Do M nằm trên \(\Delta:3x-y+1=0\) nên \(M\left(m;3m+1\right)\). Ta có \(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|3\overrightarrow{MG} \right|\) \(=3MG\)
Gọi I là tâm tỉ cự của 2 điểm A, B ứng với bộ số \(\left(1;2\right)\) \(\Rightarrow\overrightarrow{IA}+2\overrightarrow{IB}=\overrightarrow{0}\). Điều này có nghĩa \(\overrightarrow{IB}=\dfrac{1}{3}\overrightarrow{AB}\). Mà \(\overrightarrow{AB}=\left(3;3\right)\) nên \(\overrightarrow{IB}=\left(1;1\right)\) \(\Rightarrow I\left(1;5\right)\)
Với điểm M, ta có \(\left|\overrightarrow{MA}+2\overrightarrow{MB}\right|=\left|\left(\overrightarrow{MI}+\overrightarrow{IA}\right)+2\left(\overrightarrow{MI}+\overrightarrow{IB}\right)\right|\) \(=\left|3\overrightarrow{MI}\right|=3MI\) (do \(\overrightarrow{IA}+2\overrightarrow{IB}=\overrightarrow{0}\))
Từ đó \(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|+\left|\overrightarrow{MA}+2\overrightarrow{MB}\right|\)
\(=3\left(MG+MI\right)\). Ta sẽ tìm GTNN của \(MG+MI\)
Ta thấy \(MG+MI\ge IG\). Ta lại có \(\left(3.2-3+1\right)\left(3.1-5+1\right)< 0\) nên I và G nằm khác phía so với đường thẳng \(\Delta:3x-y+1=0\). Do đó, \(MG+MI=IG\Leftrightarrow\) M nằm trên IG.
Phương trình đường thẳng IG: \(\dfrac{y-3}{x-2}=\dfrac{5-3}{1-2}=-2\) \(\Leftrightarrow y-3=4-2x\) \(\Leftrightarrow2x+y-7=0\).
M thuộc IG \(\Leftrightarrow2m+\left(3m+1\right)-7=0\) \(\Leftrightarrow m=\dfrac{6}{5}\) \(\Rightarrow M\left(\dfrac{6}{5};\dfrac{23}{5}\right)\)
Vậy điểm \(M\left(\dfrac{6}{5};\dfrac{23}{5}\right)\) thỏa mãn ycbt.