Câu 3. (1,5 điểm) Trong mặt phẳng tọa độ $O x y$, cho hai điểm $A(3 ;-5), B(1 ; 0)$.
a) Tìm tọa độ điểm $C$ sao cho $\overrightarrow{O C}=-3 \overrightarrow{A B}$.
b) Tìm điểm $D$ đối xứng với $A$ qua $C$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
a) Ta có: \(\overrightarrow {OA} = \left( {2;1} \right)\) ( do A(2; 1)) và \(\overrightarrow {OB} = \left( {3;3} \right)\) (do B (3; 3)).
Hai vectơ này không cùng phương (vì \(\frac{2}{3} \ne \frac{1}{3}\)).
Do đó các điểm O, A, B không cùng nằm trên một đường thẳng.
Vậy chúng không thẳng hàng.
b) Các điểm O, A, B không thẳng hàng nên OABM là một hình hành khi và chỉ khi \(\overrightarrow {OA} = \overrightarrow {MB} \).
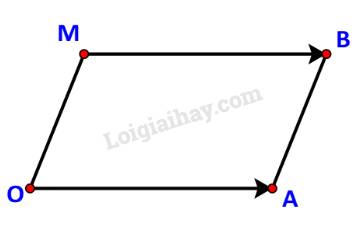
Do \(\overrightarrow {OA} = \left( {2;1} \right),\quad \overrightarrow {MB} = \left( {3 - x;3 - y} \right)\) nên
\(\overrightarrow {OA} = \overrightarrow {MB} \Leftrightarrow \left\{ \begin{array}{l}2 = 3 - x\\1 = 3 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right.\)
Vậy điểm cần tìm là M (1; 2).

Chọn A
Gọi I (a;b;c)
Ta có IA=IO=R ó hình chiếu của I lên OA là trung điểm 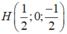 của OA.
của OA.
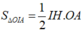
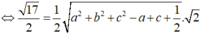
![]()
![]()
Theo bài ra ta có:
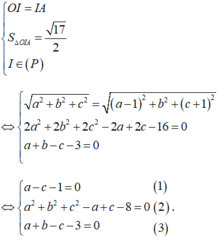
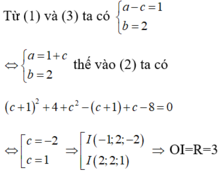
a) A(3;-5) ; B(1;0)
=> \(\overrightarrow{AB}\left(-2;5\right)\)
Gọi C(x;y) tọa độ cần tìm
khi đó \(\overrightarrow{OC}\left(x;y\right)\)
\(\overrightarrow{OC}=-3\overrightarrow{AB}\Leftrightarrow\left\{{}\begin{matrix}x=-3.\left(-2\right)=6\\y=-3.5=-15\end{matrix}\right.\)
Vậy C(6;-15)
b) D đối xứng với A qua C
=> C trung điểm AD
Gọi D(x1;y1)
Ta có : \(6=\dfrac{3+x_1}{2}\Leftrightarrow x_1=9\)
\(-15=\dfrac{-5+y_1}{2}\) <=> y1 = -25
Vậy D(9;-25)