Trong mặt phẳng xOy cho A(-2;3), B(1;5) , C(3;-7)
a) tìm N thuộc BC : S tam giác ANB= 3S tam gác ANC
b) Tìm P thuộc Ox: PA+PB nhỏ nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) có \(\widehat{xOy}+\widehat{yOz}=180^o\left(kb\right)\)
\(hay70^o+\widehat{yOz}=180^o\)
\(\Rightarrow\widehat{yOz}=180^o-70^o\)
\(\Rightarrow\widehat{yOz}=110^o\)
b) có \(\widehat{xOy}< \widehat{xOt}\left(70^o< 120^o\right)\)
=> Oy nằm giữa hai tia Ox và Ot
\(\Rightarrow\widehat{xOy}+\widehat{yOt}=\widehat{xOt}\)
\(hay70^o+\widehat{yOt}=120^o\)
\(\Rightarrow\widehat{yOt}=120^o-70^o\)
\(\Rightarrow\widehat{yOt}=50^o\)

Chọn B.
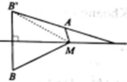
Dễ thấy A, B nằm khác phía so với mặt phẳng (xOy). Gọi B’ là điểm đối xừng với B qua (xOy). Thế thì B ' - 1 ; 4 ; 3 và M B = M B ' . Khi đó
![]()
Đẳng thức xảy ra khi và chỉ khi M, A, B’ thẳng hàng và M nằm ngoài đoạn AB’. Như vậy M cần tìm là giao điểm của đường thẳng AB’ và mặt phẳng (xOy). Đường thẳng AB có phương trình
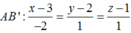
Từ đó tìm được M(5, 1, 0).

a) Ta có :
xOy' + y'Ox' =90 độ (gt)
y'Ox' + x'Oy = 90 độ (gt)
=> xOy' = 90 - y'Ox'
=> x'Oy = 90 - y'Ox'
=> xOy' = x'Oy (cùng bằng 90 - y'Ox')(dpcm)
b) Gọi Ot là pg y'Ox'(1)
=> y'Ot = x'Ot
tOy = tOx' + x'Oy
Mà y'Ot = tOx'
xOy' = x'Oy (cmt)
=> xOt = tOy
=> Ot là pg xOy (2)
Từ (1) và (2) ta có :
=> y'Ox' và xOy có cùng tia pg