Xác định parabol \(y=ax^2+bx+2\), biết rằng parabol đó :
a. Đi qua hai điểm \(M\left(1;5\right)\) và \(N\left(-2;8\right)\)
b. Đi qua điểm \(A\left(3;-4\right)\) và có trục đối xứng là \(x=-\dfrac{3}{2}\)
c. Có đỉnh là \(I\left(2;-2\right)\)
d. Đi qua điểm \(B\left(-1;6\right)\) và tung độ của đỉnh là \(-\dfrac{1}{4}\)


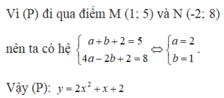
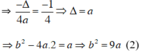
a) Vì parabol đi qua M(1; 5) nên tọa độ của M nghiệm đúng phương trình của parabol: 5 = a.12 + b.1 + 2.
Tương tự, với N(- 2; 8) ta có: 8 = a.(- 2)2 + b.(- 2) + 2
Giải hệ phương trình: ta được a = 2, b = 1.
ta được a = 2, b = 1.
Parabol có phương trình là: y = 2x2 + x + 2.
b) Giải hệ phương trình:
Parabol: y =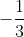 x2 - x + 2.
x2 - x + 2.
c) Giải hệ phương trình: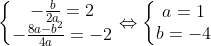
Parabol: y = x2 - 4x + 2.
d) Ta có:
Parabol: y = 16x2 + 12x + 2 hoặc y = x2 - 3x + 2.