Bài 2 : Lập phương trình đường thẳng đi qua M(2;-3) và cắt Ox, Oy tại A,B sao cho
a) OA=2/3OB
b) 4OA2 +OB2 =100
c) SOAB đạt GTLN
d) \(\frac{3}{OA^2}+\frac{2}{OB^2}=\frac{275}{36}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Gọi pt đường thẳng (d) là : \(y=ax+b\left(a\ne0\right)\)
Vì (d) có hệ số góc là 2 \(\Rightarrow a=2\Rightarrow y=2x+b\)
Vì đường thẳng d đi qua điểm \(M\left(-1;3\right)\)
\(\Rightarrow3=-2+b\Rightarrow b=5\Rightarrow y=2x+5\)
b) Gọi pt đường thẳng d là \(y=ax+b\left(a\ne0\right)\)
Vì \((d)\parallel (d')\Rightarrow a=2\Rightarrow y=2x+b\)
Vì đường thẳng d đi qua điểm \(M\left(3;5\right)\)
\(\Rightarrow5=6+b\Rightarrow b=-1\Rightarrow y=2x-1\)

c)
(d) vuông góc với (d') : y = 2x
=> (d) có dạng : y = -2x + b
(d) đi qua M (3,5) :
5 = (-2) . 3 + b
=> b = 10
(d) : y = -2x + 10

Vì (d): y=ax+b đi qua M(-2/3;-7) và N(2;1) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}-\dfrac{2}{3}a+b=-7\\2a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=-5\end{matrix}\right.\)
\(\overrightarrow{MN}\)=(8/3;8)=8/3.(1;3).
Phương trình đường thẳng cần tìm đi qua N(2;1) và nhận vectơ \(\overrightarrow{n}\)=(3;-1) làm một vectơ pháp tuyến.
MN: 3(x-2)-1(y-1)=0 \(\Leftrightarrow\) 3x-y-5=0.

(Δ) nhận 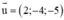 là 1 vtcp
là 1 vtcp
+ (d) cần tìm song song với (Δ)
⇒ (d) nhận 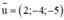 là 1 vtcp
là 1 vtcp
+ (d) đi qua M(2; 3; -5)
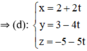

a, Vì A(1;-3) năm trên đường thẳng (d) khi tọa độ điểm B thỏa mãn phương trình đường thẳng (d)
Thay x = 1 ; y = -3 vào (d) phương trình tương đương
\(-3=5-3m+1\Leftrightarrow4-3x=-3\Leftrightarrow-3x=-7\Leftrightarrow x=\frac{7}{3}\)
b ; c thiếu đề
Bài 2 :
Vì y = x + 5 có tung độ là 2
=> y = 2 + 5 = 7
Vậy y = ( 2m - 5 )x - 5m đi qua đường thẳng y = x + 5 A( 2 ; 7 )
Thay x = 2 ; y = 7 vào y = ( 2m - 5 )x - 5m ta được :
\(7=\left(2m-5\right)2-5m\Leftrightarrow4m-10-5m=7\Leftrightarrow-m=17\Leftrightarrow m=-17\)
b/
\(4OA^2+OB^2=100\)
\(\Leftrightarrow4\left(\frac{2k+3}{k}\right)^2+\left(2k+3\right)^2=100\)
\(\Leftrightarrow4k^4+12k^3-75k^2+48k+36=0\)
\(\Leftrightarrow\left(2k-3\right)\left(2k^3+9k^2-24k-12\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}k=\frac{3}{2}\\2k^3+9k^2-24k-12=0\end{matrix}\right.\)
Rất tiếc là pt đằng sau có nghiệm nhưng ko giải được
c/
\(S_{OAB}=\frac{1}{2}OA.OB=\frac{1}{2}\left|2k+3\right|.\left|\frac{2k+3}{k}\right|=\frac{1}{2}\left|\frac{4k^2+12k+9}{k}\right|\)
\(S_{OAB}=\frac{1}{2}\left|4k+\frac{9}{k}+12\right|\)
Biểu thức này chỉ tồn tại min chứ ko tồn tại max. Đề bài ko đúng
d/ \(\frac{3k^2}{\left(2k+3\right)^2}+\frac{2}{\left(2k+3\right)^2}=\frac{275}{36}\)
\(\Leftrightarrow36\left(3k^2+2\right)=275\left(2k+3\right)^2\)
\(\Leftrightarrow992k^2+3300k+2403=0\)
\(\Rightarrow\left[{}\begin{matrix}k=-\frac{9}{4}\\k=-\frac{267}{248}\end{matrix}\right.\)
Do đường thẳng d cắt cả Ox và Oy nên có hệ số góc và tung độ gốc khác 0
Gọi pt đường thẳng có dạng
\(y=kx+b\Rightarrow2k+b=-3\Rightarrow b=-2k-3\ne0\Rightarrow k\ne-\frac{3}{2}\)
\(\Rightarrow y=kx-2k-3\)
Giao điểm của d với Oy và Ox lần lượt là: \(B\left(0;-2k-3\right)\) ; \(A\left(\frac{2k+3}{k};0\right)\)
\(\Rightarrow OA=\left|\frac{2k+3}{k}\right|\) ; \(OB=\left|2k+3\right|\)
a/ \(OA=\frac{2}{3}OB\Leftrightarrow\left|\frac{2k+3}{k}\right|=\frac{2}{3}\left|2k+3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}\frac{2k+3}{k}=\frac{2}{3}\left(2k+3\right)\\\frac{2k+3}{k}=-\frac{2}{3}\left(2k+3\right)\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}k=\frac{3}{2}\\k=-\frac{3}{2}\left(l\right)\end{matrix}\right.\)
\(\Rightarrow y=\frac{3}{2}x-6\Leftrightarrow3x-2y-12=0\)