Cho hình vuông ABCD có tâm I(4;-1) và pt 1 cạnh là 3x-y+5=0
a) Viết pt 2 đường chéo của hình vuông.
b) Viết tọa độ 4 đỉnh của hình vuông
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
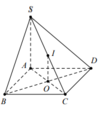
Vì O,I lần lượt là trung điểm của AC,SC. Suy ra OI//SA mà S A ⊥ A B C D ⇒ O I ⊥ A B C D .
S A ⊥ A B C D ⇒ S A ⊥ B D mà B D ⊥ A C ⇒ B D ⊥ S A C .
Ta có S A ⊥ C D A D ⊥ C D ⇒ C D ⊥ S A D ⇒ C D ⊥ S D ⇒ ∆ S C D vuông tại D.
Suy ra ID = IC tương tự ta được I B = I C ⇒ I A = I B = I C = I D .
BC không vuông góc với mặt phẳng (SCD) vì S C B ^ < 90 °
Vậy có hai khẳng định đúng là 1 và 3.

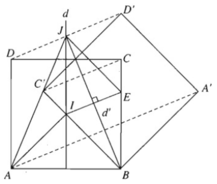
Gọi F là phép đối xứng qua đường trung trực d của cạnh AB, G là phép đối xứng qua đường trung trực d' của cạnh IE. Khi đó F biến AI thành BI, G biến BI thành BE. Từ đó suy ra phép dời hình có được bằng cách thực hiện liên tiếp hai phép biến hình F và G sẽ biến AI thành BE.
Hơn nữa gọi J là giao của d và d', thì dễ thấy JA = JB, JI = JE và 2(JI, JB) = (JI, JE) = 45 ο
(vì JE / /IB). Do đó theo kết quả của bài 1.21, phép dời hình nói trên chính là phép quay tâm J góc 45 ο
Lưu ý. Có thể tìm được nhiều phép dời hình biến AI thành BE.
b) F biến các điểm A, B, C, D thành B, A, D, C; G biến các điểm B, A, D, C thành B, A', D', C'. Do đó ảnh của hình vuông ABCD qua phép dời hình nói trên là hình vuông BA'D'C' đối xứng với hình vuông BADC qua d'