Cho hai hàm số bậc nhất y = x –2 (D1); y= mx + 1(D2). Tìm m để đồ thịcủa (D1) và (D2) cắt nhau tại điểm A có hoành độ bằng 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
9 tháng 11 2023
Bài 1
ĐKXĐ: m ≠ 0 và m ≠ -1/2
a) Để hai đường thẳng cắt nhau thì:
3m ≠ 2m + 1
⇔ m ≠ 1
Vậy m ≠ 0; m ≠ -1/2 và m ≠ 1 thì hai đường thẳng đã cho cắt nhau
b) Để hai đường thẳng song song thì:
3m = 2m + 1
⇔ m = 1 (nhận)
Vậy m = 1 thì hai đường thẳng đã cho song song
KV
9 tháng 11 2023
Bài 2
ĐKXĐ: m ≠ 0 và m ≠ -1/2
a) Để hai đường thẳng đã cho cắt nhau thì:
3m ≠ 2m + 1
⇔ m ≠ 1
Vậy m ≠ 0; m ≠ -1/2; m ≠ 1 thì hai đường thẳng đã cho cắt nhau
b) Để hai đường thẳng trùng nhau thì:
3m = 2m + 1 và 4 - m² = 3
*) 3m = 2m + 1
⇔ m = 1 (nhận) (*)
*) 4 - m² = 3
⇔ m² = 4 - 3
⇔ m² = 1
⇔ m = 1 (nhận) hoặc m = -1 (nhận) (**)
Từ (*) và (**) ⇒ m = 1 thì hai đường thẳng đã cho trùng nhau
c) Để hai đường thẳng đã cho song song thì:
3m = 2m + 1 và 4 - m² ≠ 3
*) 3m = 2m + 1
⇔ m = 1 (nhận) (1)
*) 4 - m² ≠ 3
⇔ m² ≠ 1
⇔ m ≠ 1 (nhận) và m ≠ -1 (nhận) (2)
Từ (1) và (2) ⇒ Không tìm được m để hai đường thẳng đã cho song song
d) Để hai đường thẳng vuông góc thì:
3m.(2m + 1) = -1
⇔ 6m² + 3m + 1 = 0 (3)
Ta có:
6m² + 3m + 1 = 6.(m² + m/2 + 1/6)
= 6.(m² + 2.m.1/4 + 1/16 + 5/48)
= 6(m + 1/4)² + 5/8 > 0 (với mọi m)
⇒ (3) là vô lý
Vậy không tìm được m để hai đường thẳng đã cho vuông góc
25 tháng 11 2023
a: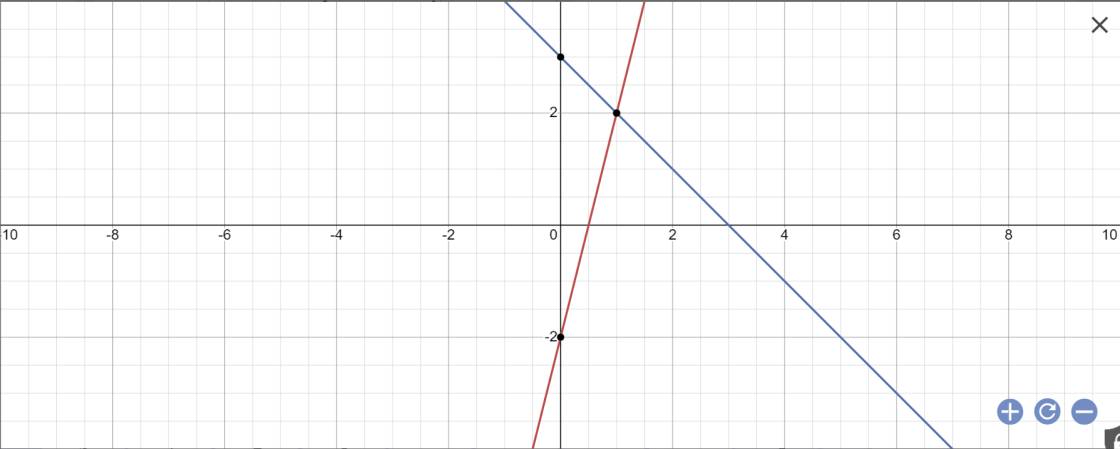 
b: Phương trình hoành độ giao điểm là:
4x-2=-x+3
=>4x+x=3+2
=>5x=5
=>x=1
Thay x=1 vào y=-x+3, ta được:
\(y=-1+3=2\)
Vậy: M(1;2)
c: Gọi \(\alpha;\beta\) lần lượt là góc tạo bởi (d1),(d2) với trục Ox
(d1): y=4x-2
=>\(tan\alpha=4\)
=>\(\alpha=76^0\)
(d2): y=-x+3
=>\(tan\beta=-1\)
=>\(\beta=135^0\)
d: Thay y=6 vào (d1), ta được:
4x-2=6
=>4x=8
=>x=2
=>A(2;6)
Thay x=6/2=3 vào (d2), ta được:
\(y=-3+3=0\)
vậy: B(3;0)
Vì (d):y=ax+b đi qua A(2;6) và B(3;0) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}2a+b=6\\3a+b=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a+b-3a-b=6-0\\3a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-a=6\\b=-3a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=-6\\b=-3\cdot\left(-6\right)=18\end{matrix}\right.\)
Vậy: (d): y=-6x+18
e: A(2;6); B(3;0); M(1;2)
\(AM=\sqrt{\left(1-2\right)^2+\left(2-6\right)^2}=\sqrt{17}\)
\(BM=\sqrt{\left(1-3\right)^2+\left(2-0\right)^2}=2\sqrt{2}\)
\(AB=\sqrt{\left(3-2\right)^2+\left(0-6\right)^2}=\sqrt{37}\)
Chu vi tam giác AMB là:
\(C_{AMB}=\sqrt{17}+2\sqrt{2}+\sqrt{37}\)
Xét ΔAMB có
\(cosAMB=\dfrac{MA^2+MB^2-AB^2}{2\cdot MA\cdot MB}=\dfrac{17+8-37}{2\cdot2\sqrt{2}\cdot\sqrt{17}}=\dfrac{-3}{\sqrt{34}}\)
=>\(\widehat{AMB}\simeq121^0\) và \(sinAMB=\sqrt{1-\left(-\dfrac{3}{\sqrt{34}}\right)^2}=\dfrac{5}{\sqrt{34}}\)
Xét ΔAMB có
\(\dfrac{AB}{sinAMB}=\dfrac{AM}{sinABM}=\dfrac{BM}{sinBAM}\)
=>\(\dfrac{\sqrt{17}}{sinABM}=\dfrac{2\sqrt{2}}{sinBAM}=\sqrt{37}:\dfrac{5}{\sqrt{34}}\)
=>\(sinABM\simeq0,58;\widehat{BAM}\simeq0,4\)
=>\(\widehat{ABM}\simeq35^0;\widehat{BAM}\simeq24^0\)
2 tháng 12 2018
a)
đường thẳng (d1) song song với đường thẳng (d2) khi :
a = a' và b khác b'
suy ra :
\(m-1=3\) \(\Leftrightarrow m=4\)
vậy đường thẳng (d1) song song với đường thẳng (d2) khi m = 4
DP
6 tháng 12 2021
a) d1//d2 ⇔\(\left\{{}\begin{matrix}3m=2m-2\\7\ne-5\end{matrix}\right.\)
⇔ m=-2
b) d1 và d2 không thể trùng nhau vì
Đk để d1 trùng d2 là \(\left\{{}\begin{matrix}a=a'\\b=b'\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}3m=2m-2\\7=-5\end{matrix}\right.\)(vô lí)
1 tháng 12 2021
\(a,\Leftrightarrow\left\{{}\begin{matrix}2-m>0\\m-4>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< 2\\m>4\end{matrix}\right.\Leftrightarrow m\in\varnothing\\ b,\Leftrightarrow2-m=m-4\Leftrightarrow m=3\\ c,\Leftrightarrow2-m\ne m-4\Leftrightarrow m\ne3\)
5 tháng 12 2021
\(\left(d_1\right)\text{//}\left(d_2\right)\Leftrightarrow\left\{{}\begin{matrix}m-3=-2m\\m^2-6\ne3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=1\\m\ne\pm3\end{matrix}\right.\Leftrightarrow m=1\\ \left(d_1\right)\cap\left(d_2\right)\text{ tại 1 điểm trên Oy}\\ \Leftrightarrow\left\{{}\begin{matrix}y=\left(m-3\right)\cdot0+m^2-6\\y=-2m\cdot0+3=3\end{matrix}\right.\Leftrightarrow m^2-6=3\\ \Leftrightarrow\left[{}\begin{matrix}m=3\\m=-3\end{matrix}\right.\\ \left(d_1\right)\equiv\left(d_2\right)\Leftrightarrow\left\{{}\begin{matrix}m-3=-2m\\m^2-6=3\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
\(\text{Phương trình hoành độ giao điểm: }x-2=mx+1\\ \text{Thay }x=1\Leftrightarrow m+1=-1\Leftrightarrow m=-2\)