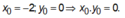Gọi ∆ là tiếp tuyến tại điểm M( x 0 ; y 0 ), x 0 < 0 thuộc đồ thị hàm số y = x + 2 x + 1 sao cho khoảng cách từ I(-1;1) đến ∆ đạt giá trị lớn nhất, khi đó x0, y0 bằng
A. -2.
B. 2.
C. -1.
D. 0.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
Do AB là đường kính \(\Rightarrow\widehat{AMB}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\widehat{AMB}=90^0\Rightarrow\Delta AMB\) vuông tại M
b.
\(\widehat{AMK}=180^0-\widehat{AMB}=90^0\Rightarrow\Delta AMK\) vuông tại M
\(\Rightarrow MD\) là trung tuyến ứng với cạnh huyền
\(\Rightarrow MD=AD\)
Xét hai tam giác OAD và OMD có: \(\left\{{}\begin{matrix}OA=OM=R\\AD=MD\left(cmt\right)\\OD\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta OAD=\Delta OMD\left(c.c.c\right)\)
\(\Rightarrow\widehat{OMD}=\widehat{OAD}=90^0\)
\(\Rightarrow DM\) là tiếp tuyến của (O).
c.
E là giao điểm 2 tiếp tuyến tại B và M \(\Rightarrow EM=EB\)
Mà \(OM=OB=R\Rightarrow OE\) là trung trực BM
\(\Rightarrow OE\) đồng thời là phân giác \(\widehat{BOM}\) hay \(\widehat{MOE}=\dfrac{1}{2}\widehat{BOM}\)
Tương tự ta có OD là phân giác \(\widehat{AOM}\Rightarrow\widehat{DOM}=\dfrac{1}{2}\widehat{AOM}\)
\(\Rightarrow\widehat{MOE}+\widehat{DOM}=\dfrac{1}{2}\left(\widehat{BOM}+\widehat{AOM}\right)\)
\(\Rightarrow\widehat{DOE}=\dfrac{1}{2}.180^0=90^0\)
Hay tam giác DOE vuông tại O
Áp dụng hệ thức lượng với đường cao OM:
\(DM.ME=OM^2\Leftrightarrow AD.BE=R^2\)

a) Vì BD là đường kính \(\Rightarrow\angle BED=90\)
Vì MB,MA là tiếp tuyến \(\Rightarrow\Delta MAB\) cân tại M và MO là phân giác \(\angle AMB\)
\(\Rightarrow MO\bot AB\Rightarrow\angle MHB=90\)
Ta có: \(\angle MHB=\angle MEB=90\Rightarrow MEHB\) nội tiếp
Xét \(\Delta MAE\) và \(\Delta MDA:\) Ta có: \(\left\{{}\begin{matrix}\angle MAE=\angle MDA\\\angle DMAchung\end{matrix}\right.\)
\(\Rightarrow\Delta MAE\sim\Delta MDA\left(g-g\right)\Rightarrow\dfrac{MA}{ME}=\dfrac{MD}{MA}\Rightarrow MA^2=MD.ME\)
b) MEHB nội tiếp \(\Rightarrow\angle MHE=\angle MBE=\angle MDB\)
Vì \(\Delta MBD\) vuông tại B có \(MB=BD=2R\Rightarrow\Delta MBD\) vuông cân tại B
\(\Rightarrow\angle MDB=45\Rightarrow\angle MHE=45\)
c) Xét \(\Delta MOB\) và \(\Delta BAF:\) Ta có: \(\left\{{}\begin{matrix}\angle MBO=\angle BFA=90\\\angle BOM=\angle BAF=\dfrac{1}{2}\angle BOA\end{matrix}\right.\)
\(\Rightarrow\Delta MOB\sim\Delta BAF\left(g-g\right)\Rightarrow\dfrac{AF}{AB}=\dfrac{OB}{MO}=\dfrac{OD}{MO}\left(1\right)\)
Vì \(\Delta MBD\) vuông cân tại B có \(BE\bot MD\Rightarrow\angle EBD=45\)
mà \(\Delta BFK\) vuông tại F \(\Rightarrow\Delta BFK\) vuông cân tại F \(\Rightarrow\angle BKF=45\)
Xét \(\Delta BAK\) và \(\Delta MOD:\) Ta có: \(\left\{{}\begin{matrix}\angle ABK=\angle DOM\left(MEHBnt\right)\\\angle BKA=\angle MDO=45\end{matrix}\right.\)
\(\Rightarrow\Delta MOD\sim\Delta BAK\left(g-g\right)\Rightarrow\dfrac{AK}{AB}=\dfrac{OD}{MO}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\dfrac{AK}{AB}=\dfrac{AF}{AB}\Rightarrow AK=AF\Rightarrow\) đpcm


Đáp án C
Phương trình tiếp tuyến của (C) tại M k x k ; y k là y = y k = y ' x k x - x k
⇔ y = y ' x k x - x k + y k = 3 x k 2 - 2018 x - x k + x k 3 - 2018 x k ( d )
Phương trình hoành độ giao điểm của (C) và tiếp tuyến (d) là
x 3 - 2018 x = 3 x k 2 - 2018 x - x k + x k 3 - 2018 x k ⇔ x - x k x 2 + x k x - 2 x k 2 = 0 ⇔ [ x = x k x = - 2 x k Do đó x k + 1 = - 2 x k suy ra x 1 = 1 ; x 2 = - 2 ; x 3 = 4 ; . . . ; x n = ( - 2 ) n - 1 ( cấp số nhân với q = -2)
Vậy 2018 x n + y n + 2 2019 = 0 ⇔ x n 3 = - 2 2019 ⇔ - 2 3 n - 3 = - 2 2019 ⇒ n = 674

Chọn đáp án B
Ta có y ' = 3 x 2 - 11 . Giả sử M m ; m 3 - 11 m thì tiếp tuyến ∆ của (C) tại điểm M có hệ số góc là k = y ' m = 3 m 2 - 11
Phương trình ∆ : y = 3 m 2 - 11 x - 2 m .
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng ∆ là:
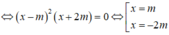
Suy ra hoành độ các điểm Mn lập thành một cấp số nhân (xn) có số hạng đầu x 1 = - 2 và công bội q = -2.
Ta có x n = x 1 . q n - 1 = - 2 n
![]() .
.
Để 11 x n + y n + 2 2019 = 0
⇔ 3 n = 2019 ⇔ n = 673
Chọn D.
Gọi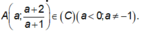
Phương trình tiếp tuyến của (C) tại A là:
=> M(-2;0)
Suy ra