Cho phương trình ; x2 +4mx -4[m+1] =0 [ với m là tham số]
a , Chứng minh rằng phương trình luôn có 2 nghiệm phân biệt với mọi giá trị của m
b , Gọi x1 và x2 là 2 nghiệm của phương trình , tìm giá trị của m để biểu thức T= [x1 -x2]2 đạt giá trị nhỏ nhất

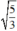 và x = -
và x = -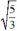


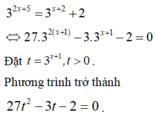
\(x^2+4mx-4\left(m+1\right)=0\left(1\right)\) \(\Rightarrow\) \(\Delta'=\left(2m+1\right)^2+3>0\) ; \(\forall m\)
pt (1)
luôn có 2 nghiệm phân biệt
\(T=x_1^2+x_2^2-2x_1x_2=\left(x_1+x_2\right)^2-4x_1x_2\)
x1 ;x2 là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=-4m\\x_1x_2=-4\left(m+1\right)\end{matrix}\right.\Rightarrow T=16m^2+16m+16\)
\(\Leftrightarrow T=16\left(m+\dfrac{1}{2}\right)^2+12\ge12\)
\(\Rightarrow T_{min}=12\) đạt được khi m = - \(\dfrac{1}{2}\)
cau a :\(x^2+4mx-4\left(m+1\right)=0\left(1\right)\)
\(\Delta'=\left(2m+1\right)^2+3>0\) ; \(\forall m\) \(\Rightarrow\left(1\right)\)luôn có 2 nghiệm phân biệt
cau b :T =\(\left(x_1-x_2\right)^2=x_1^2+x_2^2-2x_1x_2=\left(x_1+x_2\right)^2-4x_1x_2\)
lao co \(\left\{{}\begin{matrix}x_1+x_2=-2m\\x_1x_2=-4\left(m+1\right)\end{matrix}\right.thayvaoT\) .(x1 ;x2 là 2 nghiệm của (1) )
\(\Rightarrow T=4m^2+16m+16=\left(2m+4\right)^2\ge0\)
\(\Rightarrow\)Tmin = 0 đạt được khi m = -2