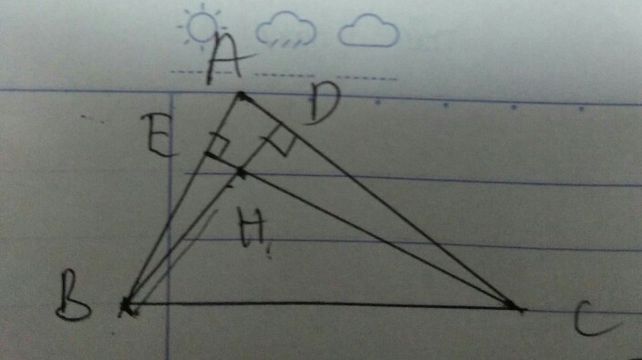
Tam giác nhọn ABC, có AB<AC. Các đường cao BE và CF cắt nhau tại O. Trên tia đối của tia BE lấy điểm G sao cho BG=AC; trến tia đối của tia CF lấy điểm H sao cho CH=AB
a)Chứng minh tam giác AGB= tam giác HAC
b)Chứng minh AG vuông góc với AH
c)Gọi M là trung điểm của GH, N là giao điểm của BC và GH
- Chúng minh góc OAM= góc BNG
- So sanh số đo của hai góc BAM và MAC

Mọi người tk mình đi mình đang bị âm nè!!!!!!
Ai tk mình mình tk lại nha !!!
a) Xét tam giác ABE vuông tại E và tam giác ACF vuông tại F có:
BAC+ABE=90 BAC+ACF=90
=> ABE=ACF
=> 180-ABE=180-ACF =>ABG=HCA
Xét tam giác AGB và tam giác HAC có:
AB=HC (gt)
ABG=HCA (CMT)
GB=AC (gt)
=> Tam giác AGB= Tam giác HAC (c.g.c) (ĐPCM)
b)Theo a có:Tam giác AGB= Tam giác HAC
=> GAB=AHC (hai góc tương ứng)
Xét tam giác AFH vuông tại F có :
FAH+AHC=90 (định lí tổng 3 goác 1 tam giác )
=> FAH+GAB=90 (vì GAB=AHC cmt)
=>GAH=90 => AG vuông góc với AH (ĐPCM)
c) 1)Theo a, có: Tam giác AGB= Tam giác HAC
=> AG=HA ( hai cạnh tương ứng)
=> Tam giác AGH cân tại A
Mà M là trung điểm của GH => AM là trung tuyến đồng thời là đường cao
=> AM vuông góc với GH
=> AMN=90 =>Tam giác MIN vuông tại M
=>MIN+IMN+MNI=180 (định lí tổng ba góc 1 tam giác)
=>MNI=180-90-MIN=90-MIN (1)
Gọi giao điểm của AO và BC là K, giao điểm của AM và BC là I
Vì O là giao điểm hai đường vuông góc BE và CF của tam giác ABC nên AO là đường vuông góc thứ ba của tam giác này
=> AKN=90 => Tam giác AKI vuông tại K
=> IAK+AKI+AIK=180
=>IAK=180-90-AIK=90-AIK (2)
Từ (1) và (2) có: MNI=90-MIN, IAK=90-AIK
Mà MIN và AIK đối đỉnh => MNI=IAK =>BNG=OAM (ĐPCM)
2) Ta có AB < AC mà AC = BG
=> AB < BG
=>AGB < GAB mà AGB = HAC (câu a)
=>HAC < GAB (1)
Tam giác AGH cân tại A, đường trung tuyến AM
=> GAM = HAM (2).
Từ (1) và (2) => BAM = GAM - GAB < HAM - HAC = MAC (ĐPCM)