Cho đường tròn tâm O bán kính 5cm; đường kính AB; tiếp tuyến Bx. Gọi C là một điểm trên đường tròn sao cho \(\widehat{BAC}=30^o\). Tia AC cắt Bx ở E.
a) Chứng minh: \(BC^2=AC.CE\)
b) Tính BE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án đúng là câu B
P/s các bạn có thể nhầm câu A với câu B nên mình xin giải thích là đường tròn là phần bên ngoài của hình tròn

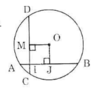
a) Kẻ OJ vuông góc với AB tại J.
Theo quan hệ vuông góc giữa đường kính và dây suy ra: J là trung điểm của AB.
![]()
Áp dụng định lí Pitago trong tam giác vuông OAJ có:
OJ2 = OA2 – AJ2 = 52 – 42 = 9 (OA = R = 5cm)
=> OJ = 3cm (1)
Vậy khoảng cách từ tâm O đến dây AB là OJ = 3cm.

 ∆OBH vuông tại H
∆OBH vuông tại H
⇒ OB² = OH² + BH² (Pytago)
⇒ BH² = OB² - OH²
= 5² - 4²
= 9
⇒ BH = 3 (cm)
Do OH ⊥ AB
⇒ H là trung điểm của AB
⇒ AB = 2BH = 2.3 = 6 (cm)
Gọi OH là khoảng cách từ tâm O đến dây AB
=>OH\(\perp\)AB tại H
=>OH=4cm
ΔOAB cân tại O
mà OH là đường cao
nên H là trung điểm của AB
ΔOHA vuông tại H
=>\(OH^2+HA^2=OA^2\)
=>\(HA^2+4^2=5^2\)
=>\(HA^2=5^2-4^2=9\)
=>HA=3(cm)
H là trung điểm của AB
=>\(AB=2\cdot AH=6\left(cm\right)\)

Mình chỉ nêu cách giải thôi nha, ko có biết trình bày đâu à
Câu 1 (bạn tự vẽ hình và xem câu trả lời của mình có ổn không nhé)
a. - ta có góc A = 90.
- Xét tam giác BEH, áp dụng định lí tam giác có đường trung tuyến ứng vs cạnh huyền bằng nửa cạnh huyền là tam giác vuông (IE = IB = IH = R đường tròn tâm I = BH/2). Ta có góc BEH bằng 90, suy ra góc AEH bằng 90 vì kề bù.
- Chứng minh tương tự với tam giác CHF, ta có góc F bằng 90.
=> Xét tứ giác AEHF ta có A = E = F = 90 theo cmt, nên AEHF là hình chữ nhật.
- vì AEHF là hình chữ nhật nên AH = EF. Áp dụng hệ thức lượng tính ra AH = căn của AB.AC = căn 48 = 4 căn 3.
b, Xét hình chữ nhật AEHF, gọi giao điểm của hai đường chéo là O. Áp dụng các tính chất của hình chữ nhật (hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường), cm được OA = OE = OF = OH. O là tâm, bán kính là OA = OE = OF = OH.
c. Trước hết, KF giao EF tại F.
*. Cm góc OFK bằng 90.
- KH = KF = bán kính đường tròn tâm K. Suy ra KHF cân tại K, góc KHF = KFH.
- OF = OH theo cm ở câu b, nên OHF = OFH.
Nên KFH + OFH = KHF + OHF = 90.
Mà KFH + OFH = OFK. => OFK = 90.
Kết luận : KF là tiếp tuyến.
Câu 2
- Lấy I là trung điểm OA.
Xét tam giác vuông OBA (góc B = 90 vì AB là tiếp tuyến), ta có IO = IA ( I là trung điểm) = IB (định lí). Cm tương tự, IO = IA = IC.
=> I là tâm đường tròn cần tìm, bán kính là IA/2.
- Áp dụng định lí Pytago, tìm được OB.
Câu 3
Để hai đồ thị vuông góc với nhau thì a.a' = -1
=> a = -1.
Để đồ thị đã cho đi qua M thì toạ độ của M thoả mãn phương trình đồ thị đó.
Thay x = -1, y =4 vào phương trình đã cho, ta có
y = ax + b <=> -1.-1 + b = 4 <=> b = 3.
Vậy a = -1, b = 3.
Câu 4
đồ thị đã cho sẽ đi qua 2 điểm là (0 ; b) = (0 ; -2m) và (-b/a ; 0) = (2 ; 0)
Suy ra đồ thị giao với trục hoành tại điểm 2 => OA = 2.
Để tam giác có diện tích là 2, đoạn OB phải có độ dài là
OA.OB : 2 = 2
=> OB = 4 : 2 = 2. bạn tính tiếp nha vì câu này thì mình ko chắc kết quả đúng ko nữa, mình dốt hàm số tệ
Câu 5
a, Áp dụng hệ thức lượng số 2 trong sgk, tính ra AH = căn 30.
Áp dụng định lí Pytago, tính được BC = căn 61
Áp dụng hệ thực lượng số 1 trong sgk, tính được BH = 25 : căn 61 và CH = 36 : căn 61.
Tâm đường tròn ngoại tiếp tam giác ABC là giao điểm 3 đường trung trực là trung điểm cạnh huyền (tam giác ABC vuông), suy ra bán kính đường tròn ngoại tiếp là căn 61 : 2.
b, Cm tứ giác là hình chữ nhật thì làm giống câu 1, phần a.
Đặt các điểm I, K tương tự như câu 1, cm vuông góc cũng giống câu 1 ấy mà.

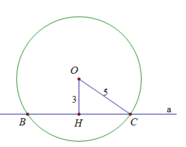
Đường thẳng a cắt đường tròn (O) tại 2 điểm phân biệt, vì khoảng cách d < R