Một chất điểm dao động điều hòa theo phương trình x = 4 cos 2 π t 3 (x tính bằng cm; t tính bằng s). Kể từ t = 0, chất điểm đi qua vị trí có li độ x = ‒2 cm lần thứ 2011 tại thời điểm
A. 3015s
B. 6030s
C. 3016s
D. 6031s
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
T = 2π/ω = 0,4 s
t = 1 s = 2T + T/2
Trong mỗi chu kì, có 2 lần chất điểm đi qua vị trí có li độ
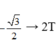 đi qua 4 lần.
đi qua 4 lần.
Ban đầu chất điểm ở vị trí1/2 cm theo chiều âm, sau T/2 chu kì, chất điểm ở vị trí -3 cm theo chiều dương → có 2 lần đi qua vị trí 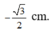 .
.
→ có tất cả 6 lần

Dao động này có biên độ \(A=5cm\)
Tần số góc là \(5\pi\left(rad/s\right)\)
Chu kì \(T=\dfrac{2\pi}{\omega}=0,4s\)
Và tần số là: \(f=\dfrac{1}{T}=\dfrac{1}{0,4}=2,5Hz\)
⇒ Chọn B

Đáp án C
Tại t = 0 chất điểm đi qua vị trí biên âm.
Trong mỗi chu kì, chất điểm đi qua vị trí x = - 2 cm hai lần.
Ta tách 2011 = 2010 + 1
Từ hình vẽ, ta thu được:
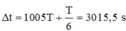


Đáp án D
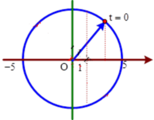
Chu kì dao động của chất điểm: T = 2s
Thấy rằng: t = 15s = 7T + T/2
Từ hình vẽ thấy rằng sau thời gian t = 7T + T/2 thì chất điểm đi qua vị trí x = 1 cm số lần là N = 2.7 + 1 = 15 lần

Đáp án A
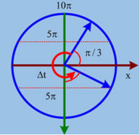
Chu kì T = 2 π ω = 2 s
Ta có: 2019 = 4 . 504 + 3
Suy ra: t = 504 T + Δ t
Từ VTLG ta có: Δ t = 3 T 4
Vậy: t = 504 T + 3 T 4 = 1009 , 5 s