Cho hình bình hành ABCD với A(3;4),B(5;6),C(8;2).Gọi D; là ảnh của D qua phép tịnh tiến vecto v=(-2;1) . Tính khoảng cách từ gốc tọa độ O đến đường thẳng BD' .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
Giả sử D(a;b;c).Vì ABCD là hình bình hành nên
![]()
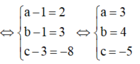
![]()
Diện tích hình bình hành ABCD là
![]()

Đáp án C
Giả sử D a ; b ; c .Vì ABCD là hình bình hành nên
C D → = B A → = 2 ; 3 ; − 8 ⇔ a − 1 = 2 b − 1 = 3 c − 3 = − 8 ⇔ a = 3 b = 4 c = − 5
⇒ D 3 ; 4 ; − 5 . Ta có: A B → − 2 ; − 3 ; 8 , A D → 1 ; 3 ; − 2
Diện tích hình bình hành ABCD là: S = A B → , A D → = 349 .

Đáp án A
Giả sử D a ; b ; c .
Vì ABCD là hình bình hành nên C D → = B A → = 2 ; 3 ; − 8 ⇔ a − 1 = 2 b − 1 = 3 c − 3 = − 8 ⇔ a = 3 b = 4 c = − 5
⇒ D 3 ; 4 ; − 5
Ta có A B → = − 2 ; − 3 ; − 8 , A D → = 1 ; 3 ; − 2
Diện tích hình bình hành ABCD là: S = A B → , A D → = 349

Chọn A.
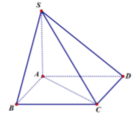
Ta có ABCD là hình bình hành => AB//CD
Do đó (SB,CD) = (SB,AB) = SBA
Vì SA ⊥ (ABCD) => SA ⊥ AB => ∆ SAB vuông tại A.
Xét tam giác vuông SAB ta có: ![]()
Vậy (SB;CD) = 60 °
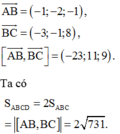
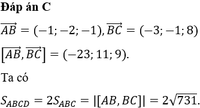
Gọi \(D\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(2;2\right)\\\overrightarrow{DC}=\left(8-x;2-y\right)\end{matrix}\right.\)
\(\overrightarrow{AB}=\overrightarrow{DC}\Rightarrow\left\{{}\begin{matrix}8-x=2\\2-y=2\end{matrix}\right.\) \(\Rightarrow D\left(6;0\right)\)
\(\overrightarrow{DD'}=\overrightarrow{v}=\left(-2;1\right)\Rightarrow D'\left(4;1\right)\) \(\Rightarrow\overrightarrow{D'B}=\left(1;5\right)\)
\(\Rightarrow\) Đường thẳng BD' nhận \(\left(5;-1\right)\) là 1 vtpt
Pt BD': \(5\left(x-5\right)-1\left(y-6\right)=0\Leftrightarrow5x-y-19=0\)
\(\Rightarrow d\left(O;BD'\right)=\frac{\left|-19\right|}{\sqrt{5^2+\left(-1\right)^2}}=\frac{19}{\sqrt{26}}\)