Cho tg ABC có góc A = 110o; góc C = 30o. Vẽ ra ngoài tg DAC có góc DAC = góc DCA = 50o
C/M tg ABD cân.
Giúp mình nhé, mình cần gấp lắm.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 12 2020
a) Xét \(\Delta AIBvà\Delta KICcó\)
AI=KI( giả thiết)
\(\widehat{AIB}=\widehat{KIC}\) (2 góc đối đỉnh)
IB=IC(vì I là trung điểm của BC )
\(\Rightarrow\Delta AIB=\Delta KIC\left(c-g-c\right)\)
vậy \(\Delta AIB=\Delta KIC\)
b)vậy \(\Delta AIB=\Delta KIC\)(chứng minh câu a )
\(\Rightarrow\widehat{KCI}=\widehat{ABI}\) ( 2 góc tương ứng )
hay \(\widehat{KCB}=\widehat{ABC}\) mà 2 góc này là 2 góc so le trong của đường thẳng CB cắt 2 đường thẳng CK và AB
\(\Rightarrow CK//AB\)
\(\Rightarrow\widehat{AC}K+\widehat{BAC}=180độ\) (2 góc trong cùng phía )
\(\Rightarrow\widehat{ACK}+110độ=180độ\)
\(\Rightarrow\widehat{ACK}=180độ-110độ=70độ\)
Vậy\(\widehat{ACK}=70độ\)
26 tháng 12 2020
a) Xét \(\Delta AIBvà\Delta KICcó\)
AI=KI( giả thiết)
\(\widehat{AIB}=\widehat{KIC}\) (2 góc đối đỉnh)
IB=IC(vì I là trung điểm của BC )
\(\Rightarrow\Delta AIB=\Delta KIC\left(c-g-c\right)\)
vậy \(\Delta AIB=\Delta KIC\)
b)vậy \(\Delta AIB=\Delta KIC\)(chứng minh câu a )
\(\Rightarrow\widehat{KCI}=\widehat{ABI}\) ( 2 góc tương ứng )
hay \(\widehat{KCB}=\widehat{ABC}\) mà 2 góc này là 2 góc so le trong của đường thẳng CB cắt 2 đường thẳng CK và AB
\(\Rightarrow CK//AB\)
\(\Rightarrow\widehat{AC}K+\widehat{BAC}=180độ\) (2 góc trong cùng phía )
\(\Rightarrow\widehat{ACK}+110độ=180độ\)
\(\Rightarrow\widehat{ACK}=180độ-110độ=70độ\)
Vậy\(\widehat{ACK}=70độ\)
CM
24 tháng 12 2017
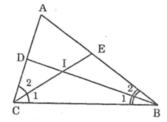
Ta có:
+ Trong ΔBIC có ∠BIC = 180º - (∠B1 + ∠C1) (1)
+ BI, CI là phân giác của ∠ABC và ∠BCA nên:
∠B1 = 1/2. ∠BAC; ∠C1 = 1/2. ∠ACB
⇒ ∠B1 + ∠C1 = 1/2. (∠BAC + ∠BCA) (2)
+ Trong ΔABC có: ∠BAC + ∠BCA = 180 - ∠A =140º (3).
Từ (1), (2) và (3) suy ra ∠BIC = 180º - 1/2.140º = 110º
Chọn đáp án C
27 tháng 1 2021
a)Vì ABC cân tại A (gt) => AB = AC (TC Tg cân)
BH vg góc AC (gt) => ^AHB=^CHB = 90o
CK vg góc AB (gt) => ^AKC=^BKC = 90o
Xét tg ABH và tg ACK:
^AHB = ^AKC (= 90)
^A chung
AB = AC (cmt)
=> tg ABH = tg ACK (ch - gn)
b) Xét tg BKC và tg CHB :
^BKC = ^CHB (=90)
BC chung
^B = ^C (tg ABC cân tại A)
=> tg BKC và tg CHB (ch - gn)
=> ^KCB = ^HBC (2 góc tương ứng)
hay ^OBC = ^OCB
=> tg OBC cân tại O (đpcm)
c) tg BKC và tg CHB (cmt) => BK = CH (2 cạnh tương ứng)
Ta có: ^B = ^ABH + ^CBH
^C = ^ACK + ^BCK
Mà ^B = ^C (tg ABC cân tại A); ^CBH = ^BCK(cmt)
=> ^ABH = ^ACK
Xét tg OBK và tgOCK:
^BKO = ^CHO (=90)
BK = CH (cmt)
^KBO = ^HCO (^ABH = ^ACK)
=> tg OBK = tg OCK (gcg)
27 tháng 1 2021
a) Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC(ΔABC cân tại A)
\(\widehat{BAH}\) chung
Do đó: ΔABH=ΔACK(cạnh huyền-góc nhọn)
b) Ta có: ΔABH=ΔACK(cmt)
nên \(\widehat{ABH}=\widehat{ACK}\)(hai góc tương ứng)
Ta có: \(\widehat{ABH}+\widehat{CBH}=\widehat{ABC}\)(tia BH nằm giữa hai tia BA,BC)
\(\widehat{ACK}+\widehat{BCK}=\widehat{ACB}\)(tia CK nằm giữa hai tia CA,CB)
mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy trong ΔABC cân tại A)
và \(\widehat{ABH}=\widehat{ACK}\)(cmt)
nên \(\widehat{CBH}=\widehat{BCK}\)
hay \(\widehat{OBC}=\widehat{OCB}\)
Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)(cmt)
nên ΔOBC cân tại O(Định lí đảo của tam giác cân)
c)
Sửa đề: ΔOBK=ΔOCH
Xét ΔOBK vuông tại K và ΔOCH vuông tại H có
OB=OC(ΔOBC cân tại O)
\(\widehat{OBK}=\widehat{OCH}\)(cmt)
Do đó: ΔOBK=ΔOCH(cạnh huyền-góc nhọn)