Hàm số y = f (x) được xác định như sau: Ứng với mỗi số tự nhiên có ba chữ số là tổng các chữ số của số đã cho.
a) Tính f (124); f (212); f (999).
b) Tìm x, biết f (x) = 3.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

f (x) = [x] = phần nguyên của x : là số nguyên lớn nhất nhỏ hơn x
h(x) = {x} = x - [x] = phần lẻ của x
1) x = -4,2 => [x] = -5 => h(-4,2) = {-4,2} = -4,2 - (-5) = 0,8
các số còn lại tương tự

f(12)=3,f(29)=11,f(73)=10
x=14,23,32,41,-83,-38,-16,-27,-38,-49,-94.-83.-61

Đáp án C
Ta có f ' x = 0 ⇔ x = 1 ; 2 ; 3 ⇒ hàm số có 3 điểm cực trị
Lại có g x = f x - m - 2018 ⇒ g ' x = f ' x = 0 ⇒ có 3 nghiệm phân biệt
Suy ra phương trình f x = m + 2018 có nhiều nhất 4 nghiệm
Xét y = f x + 1 ⇒ y ' = f ' x + 1 < 0 ⇔ [ x + 1 ∈ 1 ; 2 x + 1 ∈ 3 ; + ∞ ⇔ [ 0 < x < 1 x > 2
Suy ra hàm số y = f(x + 1) nghịch biến trên khoảng (0;1).

Đáp án B
Phương pháp: Từ đồ thị hàm số y = f’(x) lập BBT của đồ thị hàm số y = f(x) và kết luận.
Cách giải: Ta có 
BBT:
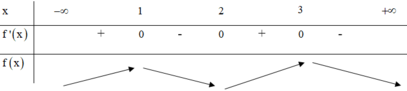
Từ BBT ta thấy (I) đúng, (II) sai.
Với ![]() => Hàm số y = f(x+1) nghịch biến trên khoảng (0;1).
=> Hàm số y = f(x+1) nghịch biến trên khoảng (0;1).
=>(III) đúng.
Vậy có hai khẳng định đúng