Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Nửa chu vi tam giác ABC là:
\(\dfrac{2+3+4}{2}=4,5\left(cm\right)\)
Diện tích tam giác ABC là:
\(S_{ABC}=\sqrt{4,5\left(4,5-2\right)\left(4,5-3\right)\left(4,5-4\right)}\)
\(=\sqrt{4,5\cdot2,5\cdot1,5\cdot0,5}=\dfrac{3\sqrt{15}}{4}\)(cm2)
=>\(\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{3\sqrt{15}}{4}\)
=>\(2\cdot AH=\dfrac{3\sqrt{15}}{4}\)
=>\(AH=\dfrac{3\sqrt{15}}{8}\left(cm\right)\)
ΔAHB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HB^2+\dfrac{135}{64}=4\)
=>\(HB^2=\dfrac{121}{64}\)
=>HB=11/8(cm)
HB+HC=BC
=>HC+11/8=4
=>HC=4-11/8=21/8(cm)
b: Gọi BK,CE lần lượt là các đường cao ứng với các cạnh AC,AB
Vì BK\(\perp\)AC và CE\(\perp\)AB
nên \(S_{ABC}=\dfrac{1}{2}\cdot BK\cdot AC=\dfrac{1}{2}\cdot CE\cdot AB\)
=>\(\left\{{}\begin{matrix}BK\cdot\dfrac{3}{2}=\dfrac{3\sqrt{15}}{4}\\CE\cdot1=\dfrac{3\sqrt{15}}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BK=\dfrac{\sqrt{15}}{2}\left(cm\right)\\CE=\dfrac{3\sqrt{15}}{4}\left(cm\right)\end{matrix}\right.\)
c: Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{4+9-16}{2\cdot2\cdot3}=\dfrac{-1}{4}\)
=>\(\widehat{BAC}\simeq104^029'\)
Xét ΔABH vuông tại H có \(sinB=\dfrac{AH}{AB}=\dfrac{3\sqrt{15}}{16}\)
=>\(\widehat{B}\simeq46^034'\)
Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)
=>\(\widehat{ACB}+104^029'+46^034'=180^0\)
=>\(\widehat{ACB}=28^057'\)

Diện tích tam giác ABC là:
3x4:2=6(cm2)
còn phần b thì mình ko bít làm nha bn

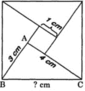
Ghép 4 tam giác vuông ABC thành một hình vuông lớn. Nhận thấy diện tích hình vuông lớn bằng 4 lần diện tích hình tam giác ABC cộng với diện tích hình vuông nhỏ ở giữa.
4 lần diện tích hình tam giác ABC là: (4 x 3 : 2) x 4 = 24cm²
Cạnh hình vuông nhỏ là: 4 – 3 = 1cm
Diện tích hình vuông nhỏ là: 1 x 1 = 1cm²
Diện tích hình vuông lớn là: 24 + 1 = 25cm²
Vì 25 = 5 x 5 nên cạnh BC của hình vuông lớn bằng 5cm.

Chu vi của hình tam giác là:
1 + 1 + 3 = 5 (cm)
Chu vi của hình tứ giác là:
3 + 4 + 7 + 11 = 25 (cm)
Chu vi hình tứ giác gấp hình tam giác số lần là:
25 : 5 = 5 (lần)
Đáp số: 5 lần

Nửa chu vi là
\(\dfrac{AB+BC+AC}{2}=\dfrac{\sqrt{13}+3\sqrt{3}}{2}\)
Diện tích tam giác ABC là \(S=\sqrt{\dfrac{\sqrt{13}+3\sqrt{3}}{2}\left(\dfrac{\sqrt{13}+3\sqrt{3}}{2}-\dfrac{\sqrt{13}}{4}\right)\left(\dfrac{\sqrt{13}+3\sqrt{3}}{2}-\dfrac{\sqrt{3}}{2}\right)\left(\dfrac{\sqrt{13}+3\sqrt{3}}{2}-\dfrac{\sqrt{3}}{4}\right)}\)

a: ha=9; hb=12; hc=16
=>hc*9=ha*16=hb*12
=>hc/16=ha/9=hb/12
=>Haitam giác này đồng dạng
b: ha=4; hb=5; hc=6
=>ha*6=24; hb*5=25; ha*4=24
=>Hai tam giác này ko đồng dạng
Bạn Chi nói đúng vì ta thấy tỉ số của 2 cạnh góc vuông và cạnh huyền là3,4,5 mà ở đây là 3,5,7.Do đó tam giác ABC không phải là tam giác vuông
Ta có: \(BC^2=7^2=49\)
\(AB^2+AC^2=3^2+5^2=34\)
Vì \(BC^2>AC^2+AB^2\) nên ΔABC không vuông
Vậy: Bạn Chi nói đúng