Cho tam giác ABC vuông tại A vẽ AI vuông góc với BC trên cạnh BC lấy K sao cho BK=AB .CMR :
a; AK là phân giác của góc CAI
b; Vẽ KH vuông góc với AC. Chứng minh AI=AH
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: 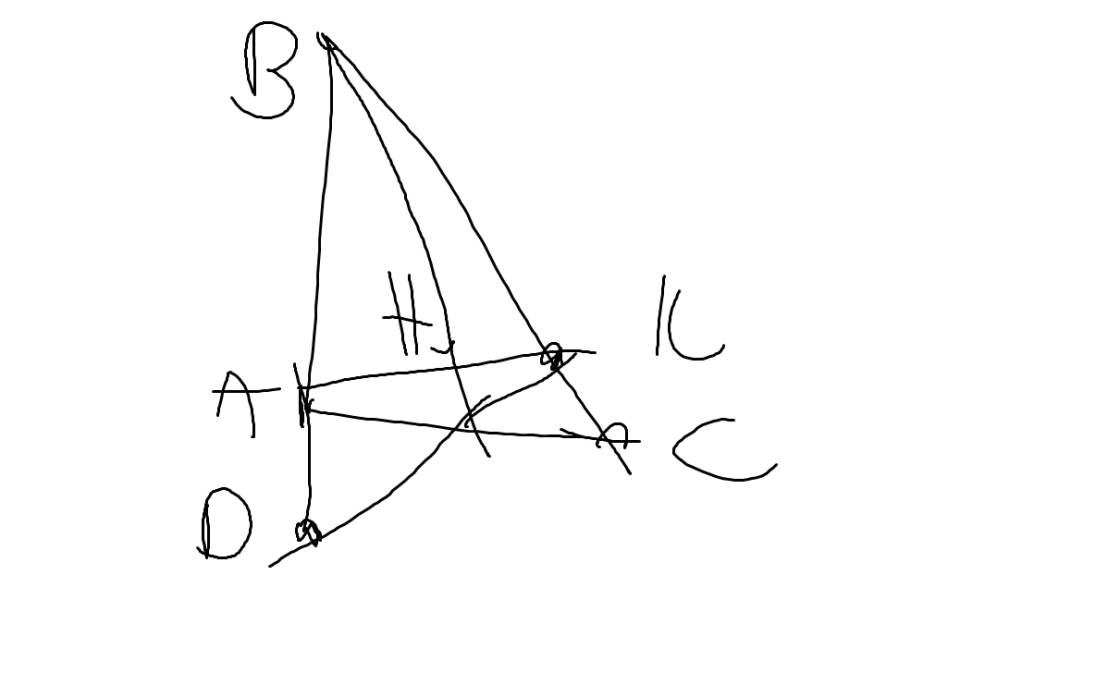
b: Xét ΔBAH và ΔBKH có
BA=BK
AH=KH
BH chung
Do đó: ΔBAH=ΔBKH
c: Sửa đề: Cm BH\(\perp\)AK
Ta có: ΔBAK cân tại B
mà BH là đường trung tuyến
nên BH là đường cao
=>BH\(\perp\)AK
d: Xét ΔBDC có \(\dfrac{BA}{AD}=\dfrac{BK}{KC}\)
nên AK//DC

Xét tam giác ABH vuông tại H, ta có: \(\widehat{BAH}=90-\widehat{ABC}\)
Xét tam giác ABC vuông tại A, ta có: \(\widehat{ACB}=90-\widehat{ABC}\)
Từ hai điều trên suy ra: \(\widehat{BAH}=\widehat{ACB}\)

a: Xét ΔBAK có BA=BK
nên ΔBAK cân tại B
b: góc BAH+góc B=90 độ
góc ACB+góc B=90 độ
=>góc BAH=góc ACB
góc HAK+góc BKA=90 độ
góc KAI+góc BAK=90 độ
mà góc BKA=góc BAK
nên góc HAK=góc KAI
d: (AH+BC)^2=AH^2+2*AH*BC+BC^2
=AH^2+2*AB*AC+AB^2+AC^2
=AH^2+(AB+AC)^2>(AB+AC)^2
=>AH+BC>AB+AC
c: AH+BC>AB+AC
=>BC-AB>AC-AH

a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
b: Ta có: ΔABD=ΔEBD
nên \(\widehat{BAD}=\widehat{BED}=90^0\)
hay DE\(\perp\)BC
c: Xét ΔADK vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)
Do đó: ΔADK=ΔEDC
Suy ra: AK=EC
Ta có: BA+AK=BK
BE+EC=BC
mà BA=BE
và AK=EC
nên BK=BC

a: Xét ΔABH và ΔKBH có
BA=BK
BH chung
HA=HK
Do đó: ΔBAH=ΔBKH
=>\(\widehat{BHA}=\widehat{BHK}\)
mà \(\widehat{BHA}+\widehat{BHK}=180^0\)(hai góc kề bù)
nên \(\widehat{BHA}=\widehat{BHK}=\dfrac{180^0}{2}=90^0\)
=>BH\(\perp\)AK tại H
=>AK\(\perp\)BI tại H
b: Sửa đề: KA là phân giác của góc IKD
Xét ΔIAK có
IH là đường trung tuyến
IH là đường cao
Do đó: ΔIAK cân tại I
Ta có: DK//AC
=>\(\widehat{DKA}=\widehat{KAI}\)
mà \(\widehat{KAI}=\widehat{IKA}\)(ΔIAK cân tại I)
nên \(\widehat{DKA}=\widehat{IKA}\)
=>KA là phân giác của góc DKI