Cho góc xOy khác góc bẹt. Trên tia Ox lấy 2 điểm A và B. Trên tia Oy lấy 2 điểm C và D. Sao cho OA=OC; OB=OD, biết BC cắt AD tại I
Chứng minh:
a, AD=CB
b, OI vuông góc với AC
Cần gấp a~~
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Giả sử A nằm giữa hai điểm O và B; C nằm giữa hai điểm O và D
Do đó ta có: OA + AB = OB; OC + CD = OD
Mà OA = OC; OB = OD (gt)
Nên AB = CD
+ Xét tam giác OAD và tam giác OCB có:
OA = OC; OB = OD (gt)
x O y ^ góc chung
Do đó: Δ O A D = Δ O C B (c – g – c)


Đáp án D

Ta có: ΔOIA và ΔOIC có
OI chung
IA = IC (chứng minh trên)
OA = OC (giả thiết)
ΔOIA = ΔOIC (c.c.c)
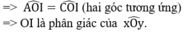

a) ΔAOD và ΔCOB có:
OA = OC (giả thiết)
Góc O chung
OD = OB (giả thiết)
⇒ ΔAOD = ΔCOB (c.g.c)
⇒ AD = BC (hai cạnh tương ứng)

Ta có hình vẽ:
a/ Xét tam giác OAD và tam giác OCB có
-O : góc chung
-OA = OC
-OB = OD
=> tam giác OAD = tam giác OCB
b/ Xét tam giác ACD và tam giác CAB có
-AC: cạnh chung
-OA = OC
OB = OD
\(\Rightarrow\)AB = CD
-AD = CB (vì \(\Delta\)OAD=\(\Delta\)OCB)
Vậy tam giác ACD = tam giác CAB

Câu hỏi của nguyenvandat - Toán lớp 7 - Học toán với OnlineMath

b,
do OA=OC, OB=OC=> AB=CD
mặt khác, xét 2 tam giác BCO và tam giác ADO
BC=AD (từ câu a)
BO=DO
CO=AO
=`> tg OBC=ODA (c.c.c) => góc OBC= góc ODA (hai góc tương ứng
xét hai tam IBA và ICD
AB=CD
góc IBA=IDC
góc BIA=DIC(hai góc đối dỉnh)
=> tg IBA=IDC(g.c.g) => IB=ID, IC=IA (các cạp cạnh tương ứng)
c,
ta đã có tg OBC= tg ODA => góc BCO = góc DAO
xét hai tg AIO và CIO
OA=OC (gt)
IA=IC
góc BCO = góc DAO
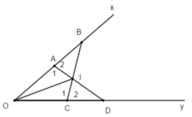
=> tg AIO= tg CIO (c.g.c) => góc IOC = góc IOA (hai góc tương ứng ) => Oi là tia phân giác của AOC hay góc xOy

- ΔAOD = ΔCOB
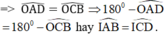
Lại có: OA = OC, OB = OD ⇒ OB – OA = OD – OC hay AB = CD.
- Xét ΔDIC và ΔBIA có:
CD = AB (chứng minh trên)
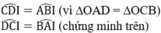
⇒ ΔDIC = ΔBIA (g.c.g)
⇒ IC = IA và ID = IB (các cặp cạnh tương ứng)
Em kham khảo link này nhé.
Câu hỏi của xukiobaby - Toán lớp 7 - Học toán với OnlineMath
Hk tốt