Cho △ ABC. G là trọng tâm △ ABC; M là trung điểm AB; N thuộc tia AC sao cho 2AN = 3AC. K thỏa mãn \(\overrightarrow{KN}+2\overrightarrow{KM}=\overrightarrow{0}\). Phân tích \(\overrightarrow{GK}\) theo \(\overrightarrow{AB},\overrightarrow{AC}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


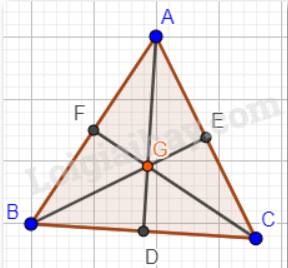
Tam giác ABC đều nên AB = AC = BC.
G là trọng tâm tam giác ABC nên AD, BE, CF là các đường trung tuyến trong tam giác.
Suy ra: AF = BF = AE = CE = BD = CD.
Xét tam giác ADB và tam giác ADC có:
AB = AC (tam giác ABC đều);
AD chung
BD = CD (D là trung điểm của đoạn thẳng BC).
Vậy \(\Delta ADB = \Delta ADC\)(c.c.c) nên \(\widehat {ADB} = \widehat {ADC}\) ( 2 góc tương ứng).
Mà ba điểm B, D, C thẳng hàng nên \(\widehat {ADB} = \widehat {ADC} = 90^\circ \)hay \(AD \bot BC\). (1)
Tương tự ta có:
\(\widehat {AEB} = \widehat {CEB} = 90^\circ \) hay\(BE \bot AC\). (2)
\(\widehat {AFC} = \widehat {BFC} = 90^\circ \) hay\(CF \bot AB\). (3)
Từ (1), (2), (3) suy ra G là giao điểm của ba đường cao AD, BE, CF.
Vậy G cũng là trực tâm của tam giác ABC.

VẼ DF VUÔNG GÓC VỚI AB, EG VUÔNG GÓC VỚI AC
BD = CE => SABC = SACE => AB.DF = AC.EG => DF/EG = AC/AB (1)
TAM GIÁC ADF ĐỒNG DẠNG VỚI TAM GIÁC AEG => DF/EG = AD/AE (2)
TỪ (1) VÀ (2) => AC/AB = AD/AE, CHO TA TAM GIÁC ABE ĐỒNG DẠNG VỚI TAM GIÁC ACD
=> GÓC ABE = GÓC ACD => TAM GIÁC ABC CÂN (đpcm)
tự vẽ hình

Hình em tự vẽ ra nhé.
Áp dụng đl pytago vào tam giác vuông ABC có:
AB^2 + AC^2 = BC^2
-- > BC = 5 (cm)
Vì tam giác ABC vuông tại A, AM là đường trung tuyến ứng với cạnh huyền BC nên ta có:
\(AM=\dfrac{1}{2}BC=\dfrac{1}{2}.5=2,5\left(cm\right)\)
Vì G là trọng tâm tâm giác ABC, ta lại có:
\(AG=\dfrac{2}{3}AM=\dfrac{2}{3}.2,5=\dfrac{5}{3}\left(cm\right)\)
bạn tự vẽ hình nhé :
Ta có: GK=\(\dfrac{1}{3}AK=\dfrac{1}{3}.\dfrac{AB+AC}{2}=\dfrac{1}{6}AB+\dfrac{1}{6}AC\)