Cho 4 điểm A, B, C, D; I, F lần lượt là trung điểm BC, CD. Chứng minh: \(2\left(\overrightarrow{AB}+\overrightarrow{AI}+\overrightarrow{FA}+\overrightarrow{DA}\right)=3\overrightarrow{DB}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 7 2016
A,B,C thẳng hàng nên A cùng nằm trên 1 đường thẳng với B và C
B,C,D thẳng hàng nên D cùng nằm trên 1 đường thẳng với B và C
=>A và D cùng nằm trên 1 đường thẳng với B và C
nên 4 điểm A,B,C và D cùng nằm trên cùng 1 đường thẳng
25 tháng 10 2015
vì khi a,b,c thẳng hàng mà b,c,d cũng thẳng hàng.Nên a,b,c,d thẳng hàng
tích đúng nha
VP
21 tháng 10 2015
(1) Do A;B;C thẳng hàng suy ra A;B;C cùng thuộc một đường thẳng
(2) Do B;C;D thẳng hàng suy ra B;C;D cùng thuộc một đường thẳng
Từ(1)và(2) suy ra A;B;C thẳng hàng
Nhớ "thich" giùm mình nha
CM
26 tháng 1 2017
Cho 4 điểm A, B, C, D cùng nằm trên đường thẳng d. Biết rằng điểm B nằm giữa hai điểm A và D, điểm C nằm giữa hai điểm B và D. Chứng tỏ rằng điểm B nằm giữa hai điểm A và C.
Vì C nằm giữa B và D è C và D nằm cùng phía với B (2)
Vì B nằm giữa A và D è A và D nằm khác phía với B (1)
Từ (1) và (2) è A và C nằm khác phía với B è B nằm giữa A và C.
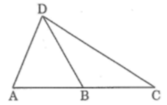
Lời giải:
Ta có:
\(\overrightarrow{AI}+\overrightarrow{FA}=\overrightarrow{AB}+\overrightarrow{BI}+\overrightarrow{FD}+\overrightarrow{DA}=\overrightarrow{AB}+\overrightarrow{DA}+\frac{1}{2}(\overrightarrow{BC}+\overrightarrow{CD})\)
Suy ra \(\text{VT}=4(\overrightarrow{AB}+\overrightarrow{DA})+\overrightarrow{BC}+\overrightarrow{CD}\)
\(\Leftrightarrow{VT}=3\overrightarrow{DB}+\overrightarrow{AB}+\overrightarrow{DA}+\overrightarrow{BC}+\overrightarrow{CD}\)
\(\Leftrightarrow{VT}=3\overrightarrow{DB}+(\overrightarrow{AB}+\overrightarrow{BC})+(\overrightarrow{CD}+\overrightarrow{DA})\)
\(\Leftrightarrow{VT}=3\overrightarrow{DB}+\overrightarrow{AC}+\overrightarrow{CA}=3\overrightarrow{DB}=\text{VP}\)
Ta có đpcm