Cho hình thang ABCD(//ABCD). E là trung điểm của AC, F là trung điểm của BD.đường thẳng EF cắt AD tại P, cắt BC tại Q.
Chứng minh PA = PD, QB=QC
Cho AB = 6cm ; FE= 5cm . Tính các độ dài CD và EQ
mng giúp mình vs mình camrmm ơnnnn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LN
14 tháng 11 2017
Hình vẽ
Vì E là trung điểm của AD và F là tung điểm cùa AC nên EF là đường trung bình của tam giác ADC và tam giác ABD
Mà P thuộc đường thẳng EF nên EP cũng là đường trung bình của tam giác ABD
Suy ra PD=PB
Vì EF là đường trung bình của tam giác ADC mà Q lại thuộc đường thẳng EQ cắt BC nên
FQ là đường trung bình của tam giác ABC
Suy ra QB=QC
Câu b)
Vì EF là đường trung bình của tam giác ADC nên
\(EF=\frac{1}{2}CD\)
Suy ra CD= 10
Vì FQ là đường trung bình của tam giác ABC nên
\(FQ=\frac{1}{2}\cdot6=3\)
Mà \(EQ=EF+FQ\)
Thay vào ta có \(EQ=5+3=8\)
Ở đây em mới hc lớp 7 thui có j thiếu anh(chị) bổ sung giùm em
NO
15 tháng 11 2017
Câu 1
Cho 
vuông tại A, D là trung điểm của BC. Gọi M là điểm đối xứng với D qua AB, E là giao điểm của DM và AB. Gọi N là điểm đối xứng với D qua AC, F là giao điểm của DN và AC.
a. Tứ giác AEDF là hình gì? Vì sao?
b. Các tứ giác ADBM, ADCN là hình gì? Vì sao?
câu 2 Cho , D là trung điểm cạnh AB, E là trung điểm cạnh AC. Tính độ dài cạnh BC, biết DE=4cm.
Bài 3: Cho hình thoi ABCD, gọi O là giao điểm cuả hai đường chéo. Vẽ đường thẳng qua B và song song với AC, vẽ đường thẳng qua C và song song với BD, hai đường thẳng đó cắt nhau ở K.
a/Tứ giác OBKC là hình gì? Vì sao?
b/Chứng minh rằng AB=OK
c/Tìm điều kiện của hình thoi ABCD để OBKC là hình vuông ?
Bài 3 Cho tam giác ABC vuông tại A có AB = 6cm , AC = 8cm , M là trung điểm của BC. Tính độ dài AM.
giúp mình với gấp lắm ạ
Thanks trước ạ
LV
24 tháng 11 2017
xet tam giac ACD co AE=ED ;AS=SC
\(\Rightarrow\)ES song song DC
ma DC song song AB
suy ra EQ song song AB
ma AS=SC
suy ra BQ=QC
b0 de kieu gi day
19 tháng 9 2019
a ) Vì \(\hept{\begin{cases}EA=ED\left(gt\right)\\FB=FC\left(gt\right)\end{cases}}\)
\(\Rightarrow\) EF là đường trung bình của hình thang ABCD.
\(\Rightarrow\) EF // AB // CD
Xét \(\Delta ABC\) có : \(\hept{\begin{cases}BF=FC\\FK//AB\end{cases}}\)
\(\Rightarrow AK=KC\)
Xét \(\Delta ABD\) có : \(\hept{\begin{cases}AE=ED\\EI//AB\end{cases}}\)
\(\Rightarrow BI=ID\)
Vậy \(\hept{\begin{cases}AK=KC\\BI=ID\end{cases}\left(đpcm\right)}\)
b ) Vì EF là đường trung bình của hình thang ABCD.
\(\Rightarrow EF=\frac{CD+AB}{2}=\frac{10+6}{8}=2\left(cm\right)\)
Mặt khác, ta có :
* EI là đường trung bình của \(\Delta ABD\)
\(\Rightarrow EI=\frac{1}{2}AB=\frac{1}{2}.6=3\left(cm\right)\)
* KF là đường trung bình của \(\Delta ABC\)
\(\Rightarrow KF=\frac{1}{2}AB=\frac{1}{2}.6=3\left(cm\right)\)
Mà : EF = EI + IK + KF
\(\Rightarrow\) IK = EF - ( EI + KF ) = 8 - ( 3 + 3 ) = 2cm.
Vậy \(\hept{\begin{cases}EI=3cm\\KF=3cm\\IK=2cm\end{cases}}\)
Chúc bạn học tốt !!!
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 8 2021
c.
K thuộc AD nên BC song song DK
Áp dụng định lý Talet: \(\dfrac{BN}{KN}=\dfrac{CN}{DN}=1\Rightarrow BN=KN\) hay N là trung điểm BK
\(\Rightarrow\) BCKD là hình bình hành (tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường)
Theo câu b, E, M, N thẳng hàng nên Q nằm trên MN (1)
Mà MN là đường trung bình của hình thang ABCD
\(\Rightarrow MN||AD\Rightarrow MN\perp AB\) (2)
Mà M là trung điểm AB (3)
(2);(3) \(\Rightarrow\) MN là trung trực AB (4)
(1);(4) \(\Rightarrow QB=QA\)
d.
Hạ CH vuông góc AD
Trong tam giác vuông CHK: \(cosKAC=\dfrac{AH}{AC}\Rightarrow AH=AC.cos\widehat{KAC}\)
Pitago: \(CH^2+AH^2=AC^2\)
Do đó: \(CK^2=CH^2+HK^2=CH^2+\left(AK-AH\right)^2=CH^2+AH^2+AK^2-2AK.AH\)
\(=AC^2+AK^2-2AK.AC.cos\widehat{KAC}\) (đpcm)
BB
10 tháng 11 2018
Đường thẳng E cắt ở đâu ý chứ nếu ghi là cắt không như thế thì hỏi trời mak chứng minh BQ=QC
10 tháng 11 2018
đường thẳng EF cắt BC tại Q nha bạn, mình viết nhầm, giúp mình giải với
CM
22 tháng 4 2017
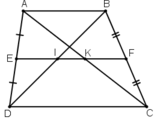
a) + Hình thang ABCD có EA = ED, FB = FC (gt)
⇒ EF là đường trung bình của hình thang ABCD.
⇒ EF // AB // CD
+ ΔABC có BF = FC (gt) và FK // AB (cmt)
⇒ AK = KC
+ ΔABD có: AE = ED (gt) và EI // AB (cmt)
⇒ BI = ID
b) + Vì EF là đường trung bình của hình thang ABCD.
⇒ EF = (AB + CD)/2 = (6 + 10)/2 = 8cm.
+ ΔABD có AE = ED, DI = IB
⇒ EI là đường trung bình của ΔABD
⇒ EI = AB/2 = 6/2 = 3(cm)
+ ΔABC có CF = BF, CK = AK
⇒ KF là đường trung bình của ΔABC
⇒ KF = AB /2 = 6/2 = 3cm
+ Lại có: EI + IK + KF = EF
⇒ IK = EF – EI – KF = 8 – 3 – 3 = 2cm