Cho hình bình hành ABCD , 2 điểm E ; F thỏa mãn 2 \(\overrightarrow{CE}+\overrightarrow{EB}=\overrightarrow{0},3\overrightarrow{DF}+\overrightarrow{BD}=\overrightarrow{0}\)
1. Chứng minh A ; E ; F thẳng hàng
2. Tìm M sao cho \(2\overrightarrow{AM}-3\overrightarrow{AF}=\overrightarrow{0}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

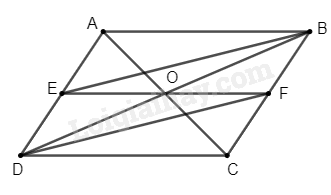
a) Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(AD = BC\); \(AD\) // \(BC\)
Mà \(E\), \(F\) là trung điểm của \(AD\), \(BC\) (gt)
Suy ra \(AE = ED = BF = FC\)
Xét tứ giác \(EBFD\) ta có:
\(ED = FB\) (cmt)
\(ED\) // \(BF\) (do \(AD\) // \(BC\))
Suy ra \(EDFB\) là hình bình hành
b) Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(O\) là trung điểm của \(AC\) và \(BD\)
Mà \(DEBF\) là hình bình hành (gt)
Suy ra \(O\) cũng là trung điểm của \(EF\)
Suy ra \(E\), \(O\), \(F\) thẳng hàng

bài này đã lm ở
https://olm.vn/hoi-dap/question/1275525.html
rùi mà
bài này đã lm tại
https://olm.vn/hoi-dap/question/1275525.html
rùi mà

A B C D E N M 1,8cm
vì MN = \(\frac{3}{4}\)DN và S(EMN) với S(EDN) có cùng chiều cao hạ từ E xuống đoạn thẳng DN
nên S(EMN) = \(\frac{3}{4}\)S(EDN) suy ra 1,8 cm2 = \(\frac{3}{4}\)S(EDN) suy ra S(EDN) = 1,8 x 4 : 3 = 2,4 cm2
vì EN = \(\frac{3}{4}\)EC và S(EDC) với S(EDN) có cùng chiều cao hạ từ D xuống đoạn thẳng EC
nên S(EDN) = \(\frac{2}{3}\)S(ECD) suy ra 2,4 cm2 = \(\frac{2}{3}\)S(ECD) suy ra S(ECD) = 2,4 x 3 : 2 = 3,6 cm2
ta có S(EDC) = EH x CD : 2 = 3,6 cm2
suy ra EH x CD = 3,6 x 2 = 7,2 cm
mà S(ABCD) = EH x CD (vì diện tích hình bình hành bằng đáy nhân chiều cao )
suy ra S(ABCD) = 7,2 cm2
đáp số 7,2 cm2
vì MN = 3434DN và S(EMN) với S(EDN) có cùng chiều cao hạ từ E xuống đoạn thẳng DN
nên S(EMN) = 3434S(EDN) suy ra 1,8 cm2 = 3434S(EDN) suy ra S(EDN) = 1,8 x 4 : 3 = 2,4 cm2
vì EN = 3434EC và S(EDC) với S(EDN) có cùng chiều cao hạ từ D xuống đoạn thẳng EC
nên S(EDN) = 2323S(ECD) suy ra 2,4 cm2 = 2323S(ECD) suy ra S(ECD) = 2,4 x 3 : 2 = 3,6 cm2
ta có S(EDC) = EH x CD : 2 = 3,6 cm2
suy ra EH x CD = 3,6 x 2 = 7,2 cm
mà S(ABCD) = EH x CD (vì diện tích hình bình hành bằng đáy nhân chiều cao )
suy ra S(ABCD) = 7,2 cm2
đáp số 7,2 cm2
k đúng cho mik
nhé
nhé

a: Xét ΔMEA và ΔMCB có
góc EMA=góc CMB
MA=MB
góc MEA=góc MCB
=>ΔMEA=ΔMCB
=>ME=MC
=>M là trung điểm của CE
Xét tứ giác AEBC có
M là trung điểm chung của AB và EC
=>AEBC là hbh
b: Để AEBC là hình chữ nhật thì góc EAC=90 độ
=>góc DAC=90 độ
=>góc ACD+góc D=90 độ
mà góc ACD=1/2*góc D
nên góc D=2/3*90=60 độ
=>góc B=60 độ
góc BAD=góc BCD=180-60=120 độ

Xét tứ giác DEBF có
DE//BF
DE=BF
Do đó: DEBF là hình bình hành